 |
 |
|
ПОЛИТОЛОГИЯ: МЕТОДЫ ИССЛЕДОВАНИЯ |
|
НАЗАД Мангейм Дж., Рич Р.К. Политология. Методы исследования ВПЕРЕД
Красным шрифтом в квадратных скобках обозначается конец текста на соответствующей странице печатного оригинала данного издания
16. СТАТИСТИКА III: ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ МЕЖДУ НЕСКОЛЬКИМИ ПЕРЕМЕННЫМИ
Одномерный и двумерный статистический анализ, описанный в предыдущих главах, часто бывают совершенно необходим для понимания объекта, который мы изучаем. Однако одномерный и двумерный анализ почти никогда не обеспечивает убедительной проверки гипотез или теорий, из которых они были извлечены. Для того чтобы проверить какую-либо гипотезу, необходимо исключить главную альтернативную конкурирующую гипотезу. И хотя четко поставленные исследовательские задачи иногда позволяют нам не принимать во внимание альтернативную гипотезу, обычно предпочитают проверять справедливость конкурирующей гипотезы, опираясь на анализ данных, а не на постановку задач исследования. А это требует
многомерного анализа, т.е. одновременного анализа взаимосвязей между тремя и более переменными. [c.438]Многие из статистических методов, уже описанных нами, могут применяться в многомерном анализе1.
Для иллюстрации мы можем использовать очень упрощенный пример и предложить метод, которым таблицы корреляции и бипараметрическая статистика могут быть адаптированы для проведения многомерного статистического анализа. Предположим, что мы хотим исследовать, какая связь существует между политическим мировоззрением и получением образования в колледже. Мы можем , предположить, что обучение в колледже дает людям некую опору для поддержания статус-кво и подготавливает их к относительно хорошему функционированию в рамках существующей социоэкономической системы. Тогда возможно мы начнем с гипотезы, что те, кто окончил колледж, будут более консервативны, чем те, кто не имел такой возможности. Чтобы проверить эту гипотезу, нам надо протестировать выборку из 50 респондентов, окончивших колледж и еще 50 таковых, в колледже не учившихся.
[c.438]Таблица 16.1.
Соотношение между получением образования в колледже и политическим мировоззрением
|
Образование |
Мировоззрение |
||
|
Либералы (%) |
Консерваторы (%) |
Общее число респондентов |
|
|
Получили |
40 (20) |
60 (30) |
(50) |
Наши гипотетические результаты представлены в табл. 16.1. Диагональное “распределение” случаев в этой таблице показывает, что можно более или менее характеризовать как консерваторов прежде всего тех, кто учился в колледже. Подсчитав критерий “хи-квадрат” для этой таблицы, мы выясним, что отношения между посещением колледжа и политическим мировоззрением статистически значимы на уровне 0,01. Все это совпадает с нашей первоначальной гипотезой.
Тем не менее, прежде чем мы рискнем представлять полученные данные в American Political Science Review, нам необходимо проверить некоторые альтернативные конкурирующие гипотезы, чтобы удостовериться, что наши результаты обоснованны. Сделать это можно несколькими способами. Один из них – это расширить наш бипараметрический анализ до многомерного анализа, который позволит нам “проконтролировать” влияние других переменных на отношение между получением образования в колледже и мировоззрением. Например, одна альтернативная конкурирующая гипотеза, достойная изучения, вытекает из наблюдения, что мужчины обычно более консервативны, чем женщины. Если в нашей выборке больше мужчин, чем женщин, то результат, представленный в табл. 16.1 может отражать различия мнений по половому признаку, а не действительное влияние образования на политические мнения.
Чтобы исследовать эту возможность, мы можем проверить отношения между образованием и воззрениями отдельно для мужчин и женщин. Тогда мы построим две табл. сопряженности – 16.2 и 16.3. Если альтернативная конкурирующая гипотеза обоснованна, то статистические отношения между этими признаками, показанные в
[c.439] табл. 16.1, не будут показаны в новых таблицах, так как влияние “мужского” или “женского” начала будет исключено. Такой процесс поддержки постоянного влияния третьей переменной на отношения между двумя другими переменными отсылает нас к процедуре контролирования и является важным шагом во всех формах многомерного анализа.В нашем случае табл. 16.2 и 16.3 на самом деле показывают, что отношения между получением образования в колледже и мировоззрением по существу одинаковы и для мужчин и для женщин. Хотя женщины в нашей выборке, как и было предсказано, не так консервативны, как мужчины, “распределение” в этих двух таблицах практически одинаково, и вычисление “хи-квадрат” критерия для каждой из них показывает, что те отношения, которые они представляют, статистически значимы. В такой ситуации исследователи говорят, что первоначально предположенные отношения “проконтролированы” и что альтернативная конкурирующая гипотеза как объяснение первоначальных данных может быть “исключена”. Если отношения достаточно хорошо выдерживают такое контролирование, они принимаются как обоснованные. Важно помнить, что мы могли бы найти такой пример, когда отношения, представленные в табл. 16.1, стали бы статистически незначимыми, и тогда мы создали бы отдельные таблицы сопряженности для мужчин и женщин. В таком случае исследователь может сказать, что первоначально предложенные отношения не прошли процедуры контроля и что альтернативная конкурирующая гипотеза не может быть исключена.
Таким образом, мы провели простейший многомерный анализ, используя технику, предназначенную для бипараметрического анализа. Мы можем продолжить эту логическую цепочку и оценить другие альтернативные конкурирующие гипотезы, применив для контролирования две или более дополнительные переменные одновременно. Чтобы проиллюстрировать это, в качестве альтернативной конкурирующей гипотезы предположим, что расовые различия между белыми и небелыми (и с точки зрения политического уровня, и с точки зрения вероятности посещения колледжа) несомненно формируют указанные в табл. 16.1 отношения между посещением колледжа и мировоззрением. Чтобы одновременно проверить влияние расовых различий и различий по половому
[c.440] признаку на указанные отношения, мы должны будем составить четыре таблицы сопряженности, представляющие эти отношения для: белых мужчин, белых женщин, небелых мужчин и небелых женщин.Таблица 16.2.
Гипотетические отношения между получением образования в колледже и политическим мировоззрением для мужчин
|
Образование |
Мировоззрение |
||
|
Либералы (%) |
Консерваторы (%) |
Общее число респондентов |
|
|
Получили |
33 (5) |
57 (20) |
(25) |
Таблица 16.3.
Гипотетические отношения между получением образования в колледже и политическим мировоззрением для женщин
|
Образование |
Мировоззрение |
||
|
Либералы (%) |
Консерваторы (%) |
Общее число респондентов |
|
|
Получили |
43 (15) |
67 (10) |
(25) |
При условии правильной обработки, такой подход к многомерному анализу может очень хорошо помочь в оценке гипотез. Однако у него есть существенные ограничения. Во-первых, он очень громоздкий, и получаемые результаты трудно интерпретировать, если используемые переменные имеют много возможных уровней. Именно поэтому непрактично применять это метод для анализа интервальных переменных; его также трудно использовать для многих номинальных и одноуровневых переменных. Например, чтобы сравнить независимую и зависимую переменную, каждая из которых содержит 5 уровней, и при этом проконтролировать их с помощью третьей переменной с 10 уровнями, потребуется анализ 10 таблиц по
[c.441] 25 ячеек в каждой. И хотя в нашем распоряжении может иметься исключительно большая и разнообразная выборка, множество ячеек в таблицах останется незаполненным, что может сделать невозможным вычисление некоторых мер связи и значимости. Мы могли бы попытаться избежать этого путем объединения определенных категорий переменных, чтобы уменьшить число уровней и сократить число необходимых таблиц и ячеек (как в том случае, когда мы сократили меру “годы учения” до дихотомии “менее 12 лет” и “12 лет и более”). Тем не менее, это означает, что имеющаяся в первоначальных данных часть информации, которая может оказаться важной, будет потеряна, что может привести к искажению результатов. Более того, с такой же проблемой мы можем столкнуться даже и после того, как мы объединили категории, – в том случае, если мы попытаемся сразу добавить для контроля несколько переменных, чтобы проверить комбинированный эффект различных переменных. Во-вторых, даже если мы можем выполнить такой анализ, его результаты трудно будет ввести в оборот, так как модель выглядит достаточно сложно, и кроме того, не существует обобщающей статистики, позволившей бы суммировать полученные в итоге данные.К счастью, существует ряд статистических приемов, которые предназначены специально для многомерного анализа и которые можно использовать для решения широкого круга задач; их результаты сравнительно легко интерпретируются. Они особенно ценны, так как обладают возможностями проверки гипотез (позволяют анализировать взаимосвязи двух переменных с учетом воздействия других переменных на каждую константу), но главное их достоинство заключено в тех способах, которыми они помогают нам уяснить сложную и хрупкую сеть взаимосвязей, в которую вплетены социальные явления. В этой главе мы познакомим вас с тремя наиболее часто используемыми способами многомерного анализа, с тем чтобы вы знали, когда и как применять их в своих исследованиях, и, читая научные труды, могли судить о том, как их применяют другие. Мы выбрали эти методы из всего множества возможных потому, что (1) они широко применяются, (2) они иллюстрируют некоторые основные принципы многомерного анализа и (3) все они основаны на
[c.442] одних и тех же базовых математических приемах и могут быть поэтому объяснены легче, чем те, которые требуют привлечения разных математических приемов. [c.443]Все, что говорилось о двумерной корреляции и регрессии в
гл.15, может быть распространено на те случаи, когда вы хотите изучить взаимосвязи между одной независимой (НП) и несколькими зависимыми переменными (ЗП). Цель множественной регрессии – обеспечить (1) подсчет независимого воздействия изменений в значениях каждой ЗП на значения НП и (2) эмпирический базис, чтобы предсказать значения зависимой переменной на основе знания совместного влияния НП.Анализ начинается с составления уравнения, которое, на ваш взгляд, точно описывает исследуемые вами причинные связи. Поскольку это уравнение можно рассматривать как
модель исследуемого процесса, это шаг расценивается как построение модели. Оно заключается в переводе вашей вербальной теории явления на язык математических уравнений. Общая формула множественной регрессии такова:Y’ = а0 + b1X1 + b2X2… +…bnXn + e.
В ней вы можете узнать несколько расширенное уравнение двумерной регрессии, описанной в
гл.15. Понимание этого уравнения может облегчить конкретный пример.Скажем, мы заинтересованы в проверке верности заявления, что выборы в сенат США могут быть “куплены” путем вклада средств в кампанию в прессе. Для этого попытаемся объяснить процент полученных кандидатом голосов следствием (1) количества средств, вложенных в рекламу в средствах массовой информации, и (2) долей среди всех имеющих право выбора людей той же партийной принадлежности, что и кандидат. Начнем со следующей простой модели процесса выборов:
Y’ = а0 + b1X1 + b2X2 + e,
где Y’ – предполагаемая доля голосов, полученных кандидатом;
а0 – среднее значение Y, если каждая независимая переменная равна 0; [c.443]
b1 – среднее изменение Y на единицу измерения Х (количество средств, вложенных в рекламу), когда воздействия остальных переменных постоянны;
X1 – количество средств, вложенных кандидатом в рекламу (в 1000 долларов);
b2 – среднее изменение Y' на единицу изменения X2 (доля выборщиков той же партийной принадлежности, что и кандидат), когда воздействия остальных переменных постоянны;
X2 – доля выборщиков той же партийной принадлежности, что и кандидат;
е – погрешность, означающая любое колебание Y1, не вызванное изменением независимой переменной в модели.
Можно попытаться проверить точность этой модели, собрав достоверные данные о борьбе за 100 мест в сенате США. Однако для того, чтобы применение методики множественной регрессии к этой или любой другой задаче оказалось удачным, необходимо, чтобы наша модель, а также данные, с помощью которых мы хотим проверить все это, удовлетворяли пяти требованиям, которые лежат в основе применения регрессии.
1. Модель должна точно соответствовать (точно описывать реальные исследуемые взаимосвязи). Для этого необходимо, чтобы (а) связь между переменными была линейна, (б) ни одна важная независимая переменная не была исключена и (в) ни одна не имеющая отношения к делу переменная не была включена.
2. Не должно быть ошибок в измерении переменных.
3. Переменные должны быть измерены в интервальной шкале.
4. Для погрешности необходимы следующие условия:
а) ее среднее геометрическое (предположительное значение для каждого наблюдения) равно 0;
б) погрешности для каждого наблюдения не коррелируют,
в) НП не коррелируют с погрешностью;
г) отклонение погрешности всегда постоянно для всех значений НП; это условие называется гомоскедастичностью;
д) погрешность имеет нормальное распределение.
5. Ни одна из НП не коррелирует четко с любой другой НП или с любой линейной комбинацией других НП. Если
[c.444] это так, то говорят, что нет четкой мультиколлинеарности2.Если наше исследование достаточно полно удовлетворяет этим условиям3, мы можем подставить вместо Y’, X1 и X2 наши конкретные значения и решить уравнение регрессии, описывающее предположения относительно неизвестных значений a1, b1 и b2 используя метод подсчета наименьших квадратов. Вот один из гипотетических результатов такого решения:
Y = 10 + 0,1 X1 + 1 X2.
[c.445]
ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Метод наименьших квадратов в случае множественной регрессии работает так же, как двумерная регрессия, в том смысле, что представляет собой проходящую через множество точек, которые представляют значения случаев по нескольким переменным, так чтобы уменьшить до минимума сумму квадратов расстояний от каждой точки до этой линии. Разница в том, что эта “прямая” в случае множественной регрессии есть множество математически обоснованных точек в системе, которая не может быть описана как двумерное множество точек, а, или точка пересечения, обычно представляет мало интереса, поскольку значения независимой переменной редко равны 0. Однако значение а, равное 10, в уравнении можно интерпретировать в том смысле, что, даже если кандидат не вкладывал средств в рекламу, и 0% избирателей в штате принадлежат к ее или его партии, он (или она) получит 10% голосов просто потому, что находится в избирательных списках.
Гораздо более важно понять смысл значений bi. Его обычно называют
частным коэффициентом регрессии; он описывает единичный вклад каждой независимой переменной в определение значений ЗП. В нашем примере о выборах значение b1, равное 0,1, можно интерпретировать как означающее, что каждые дополнительные 1000 долларов, вложенные в рекламу, увеличивают долю голосов за кандидата на одну десятую процентной единицы, а значение b2, равное 1, будет означать, что каждому 1% увеличения доли голосов тех, кто принадлежит той же партии, [c.445] соответствует 1% увеличения доли всех голосующих за кандидата. С помощью этих коэффициентов регрессия статистически сводится к постоянному влиянию любой переменной, которая воздействует как на отдельную НП, так и на ЗП через использование следующей формулы:
![]()
Такой статистический контроль заменяет тот контроль, который мы могли бы осуществлять при экспериментальном построении; он, таким образом, ценен с двух точек зрения. Во-первых, если говорить коротко, он позволяет нам оценить относительное значение различных НП для определения значений ЗП. Во-вторых, он позволяет нам исключить альтернативную гипотезу о том, что взаимосвязи между ЗП и любой конкретной НП ложны. Если мы допустим, что все значимые причины изменений ЗП включены в нашу модель, а коэффициент частичной регрессии для любой НП при этом отличен от 0 (значим)4, мы можем сделать вывод, что наличие взаимосвязи между НП и ЗП не является ложным. Если же, однако, близок к О или статистически незначим, мы должны заключить, что непосредственной связи между НП и ЗП нет. В таком случае следует исключить НП из модели, с тем чтобы сделать ее более соответствующей изучаемому объекту. Ясно, таким образом, что множественная регрессия может быть ценным инструментом в совершенствовании и улучшении наших теорий, касающихся политических явлений.
Мы можем достичь завершенности своей теории, если обратимся к подсчету коэффициента множественной детерминации, или R2 (нечто, что можно назвать множественным R2) по формуле:
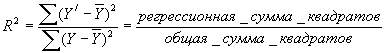
Этот коэффициент показывает, насколько близко расположены точки, обозначающие данные, вокруг “прямой”, предусмотренной нашей моделью; ее обычно называют мерой отклонений ЗП, которые могут быть объяснены колебаниями всех НП. Например, коэффициент R2, равный 0,57, можно определить как показатель того, что
[c.446] независимые переменные в модели, по которой он был посчитан, объясняют 57% колебаний зависимой переменной. R2 изменяется в пределах между 0 и 1; чем ближе он к единице, тем более совершенна наша модель. Значение R2 всегда может быть увеличено путем введения в модель добавочных НП, но исследователь должен всегда задаваться вопросом, не сделает ли вновь введенная переменная модель слишком сложной и привнесет ли она что-нибудь ценное в понимание исследуемого явления. В нашем случае с выборами, например, мы, может быть, и могли бы увеличить R2 добавлением в уравнение сведений о количестве букв в фамилии кандидата, но сделать это – значит забыть, что исследование имеет целью более полное и ценное понимание мира, а не состязание в наиболее впечатляющем применении статистики. [c.447]РЕШЕНИЕ ОБЩИХ ПРОБЛЕМ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
И данные, и сама реальность не всегда подходят для построения концептуальной модели, лежащей в основе множественного регрессионного анализа. Связи не всегда линейны, в измерениях часто бывают ошибки и т.д. К счастью, математики -статистики предусмотрели некоторые пути к тому, чтобы приспособить множественную регрессию к урегулированию подобных проблем. Мы обсудим возможности решения трех из обычно возникающих проблем, с тем чтобы вы могли (1) понять, как преодолевать такие сложности в вашем конкретном случае применения множественной регрессии, и (2) получить представление о гибкости множественной регрессии как приема статистического анализа.
Неинтервальные данные.
В социальных науках важные переменные часто не могут быть измерены в интервальной шкале, нарушая, таким образом, условие об интервальном уровне измерения. Однако неинтервальные данные могут быть использованы в множественной регрессии при двух условиях.Во-первых, если измерение является дихотомией (или может быть преобразовано в нее), его можно использовать непосредственно для регрессии, попросту придав одному значению дихотомии код 1, а другому – 0. Например, в изучении международной торговли товары можно
[c.447] классифицировать как “иностранные” и “отечественные”, приписав значению “иностранный” код 1, а значению “отечественный” – код 0. При регрессионном анализе такая схема будет восприниматься как интервальная, поскольку дихотомия имеет особые математические свойства. В результате мы можем интерпретировать частный коэффициент регрессии, посчитанный для любой закодированной дихотомически переменной, так же как мы сделали бы это в случае измерения по интервальной шкале.Неинтервальные переменные, которые имеют много категорий, могут быть приведены к виду, необходимому для множественной регрессии, путем использования системы фиктивных переменных. Рассмотрим, например, случай, где служебное положение измеряется только в категориях “высокое”, “среднее” и “низкое” в исследовании, целью которого является определение количества политических организаций, к которым принадлежит данный индивид, как функции образования (количества лет обучения) и служебного положения. Мы сможем использовать порядковые данные о профессии для множественной регрессии, если создадим две дихотомические фиктивные переменные, представляющие переменную “служебное положение”. Уравнение примет вид:
Y' = а + b1X1 + b2X2 + b3X3 +е,
где Y’ – количество политических организаций, в которых состоит участник;
Х1 – количество лет обучения;
Х2 – фиктивная переменная, принимающая значение 1, если служебное положение “низкое”, и значение 0 в остальных случаях;
Х3 – фиктивная переменная, принимающая значение 1, если служебное положение “среднее”, и значение 0 в остальных случаях.
Почему для выражения не интервальной переменной с тремя категориями используются только две фиктивные переменные? Потому что значения третьей фиктивной переменной будут точной линейной функцией двух других; таким образом, нарушится условие об отсутствии прямых мультиколлинеарных связей, и однозначный подсчет различных коэффициентов станет невозможным.
[c.448]Когда бы ни использовался принцип создания фиктивных переменных, мы должны следовать правилу создания фиктивных переменных на одну меньше, чем имеется категорий в неинтервальной переменной. Судя по практике, рекомендуется обычно не брать ту категорию, в которой наименьшее количество случаев. В нашем примере фиктивная переменная не была представлена категорией “высокое служебное положение”, потому что должностей этого уровня очень мало. Значение частного коэффициента регрессии для этой исключенной градации подсчитывается путем решения уравнения регрессии. Так, в данном примере если в каком-либо случае переменная “служебное положение принимает значение “высокое”, то значения Х1, X2 должны быть равны 0 и значение частного коэффициента регрессии для категории “высокое служебное положение” будет равно значению
Q5.Эффект взаимодействия.
Обычно регрессия наименьших квадратов предполагает, что воздействие различных НП на ЗП независимы друг от друга и для выяснения общего влияния комплекса переменных можно их просто просуммировать. На практике же влияния одних переменных усиливают и дополняют эффект воздействия других. В любом случае, когда воздействие одной НП зависит от значения другой НП, существует эффект взаимодействия. Возвращаясь к примеру о выборах, приведенному выше, мы могли бы оспорить тот факт, что расходы на рекламу имеют различные результаты в случае уже пребывающих в должности (они обычно хорошо известны) и претендентов (им еще предстоит убедить избирателей в своей пригодности).Множественную регрессию можно приспособить к этой ситуации, если представить переменную “средства, вложенные в рекламу” (X1) как результат взаимодействия между ней самой и занимаемым постом. Если мы предположим, что занимаемый пост представлен фиктивной переменной (Х3), где претенденты имеют код 1, а занимающие посты – 0, новая регрессионная модель будет выглядеть так:
Y' = а + b1X1 + b3(X1X3) + b2X2 + е,
где Х1Х3 – переменная взаимодействия, образованная произведением Х1 на Х3.
[c.449]Этот способ позволяет нам интерпретировать b1 как однократный вклад расходов на рекламу в распределение голосования путем прекращения суммарного воздействия рекламы и должности на b3 и получить таким образом более точные данные относительно значений Y.
Мультиколлинеарность. Регрессионный анализ требует, чтобы ни одна независимая переменная не была четко скоррелирована с любой другой независимой переменной или с любой линейной комбинацией независимых переменных. Обычно соблюсти это строгое требование легко, поскольку в социальных науках редко бывает так, что значения одной переменной точно выводятся из известных значений другой или ряда других переменных. Однако многие важные переменные действительно тесно связаны друг с другом. (Возьмите урбанизацию и индустриализацию, образование и доход или партии и идеологию в Западной Европе.) Если корреляция между НП в регрессионной модели достаточно велика, подсчеты коэффициента будут неточными и мы не сможем доверять результатам регрессионного анализа. Значимая мультиколлинеарность может вызвать такие большие колебания в значении частного коэффициента регрессии, что сравнивать реальные воздействия различных НП на ЗП станет невозможно. Вдобавок коэффициенты могут не достичь статистической значимости даже в тех случаях, когда наблюдается существенная взаимосвязь, что ведет к неверной констатации отсутствия двумерной связи.
Таким образом, очень важно, чтобы исследователи предпринимали серьезные попытки установить присутствие мультиколлинеарности и необходимые действия по ее корректировке. Мультиколлинеарность обычно определяют по одному или нескольким следующим признакам:
1. Высокий коэффициент R2 в уравнении, но статистически незначимые коэффициенты регрессии (b).
2. Очень сильные колебания в значениях коэффициентов регрессии (b) для одной переменной, если из уравнения выводятся или вводятся в него другие НП.
3. Значения коэффициентов регрессии, которые значительно больше или меньше (как в абсолютных значениях, так и по отношению к коэффициентам других НП), чем можно ожидать, исходя из теории и результатов других подобных исследований.
[c.450]4. Коэффициенты регрессии с неверным знаком, т.е. отрицательные тогда, когда у нас есть все основания ожидать положительного знака, и положительные тогда, когда есть основания ожидать отрицательного знака.
Если хотя бы один из этих признаков появляется при регрессионном анализе, необходима проверка на мультиколлинеарность. Это делается путем регрессирования каждой НП на все другие НП. К примеру, мы хотим проверить уравнение
Y’ = а + b1X1 +b2X2 + b3X3 + е
через такие уравнения:
X1 = а + b2X2 + b3X3;
Х2 = а + b1X1 + b3X3;
Х3 = а + b1X1 + b2X2.
Если R2 для любого из этих уравнений будет выше, чем, скажем, 0,8, мы можем заключить, что имеется значимая мультиколлинеарность.
Существует несколько способов корректировки мультиколлинеарности. Если у нас есть ряд добавочных по oотношению к выборке случаев (как, например, тогда, когда мы выбираем данные из опубликованного источника и можем просто обратиться к нему еще раз и сделать довыборку), увеличение размера выборки может в какой-то степени уменьшить мультиколлинеарность. Другой путь – определить, какие именно НП особенно тесно связаны друг с другом, и объединить их в единый фактор. Если, например, средства, вложенные в радио-, теле– и печатную рекламу, измеряются в нашем исследовании сенатских выборов отдельно, а мы обнаружим, что они тесно взаимосвязаны, можно объединить их в один признак услады в средства массовой информации, с тем чтобы уменьшить дестабилизирующее воздействие мультиколлинеарности. Естественно, любое подобное комбинирование будет работать только в том случае, если оно теоретически обосновано. Нельзя, к примеру, решать проблему мультиколлинеарности путем объединения занимаемого кандидатом поста и регионального расположения штата, поскольку теоретически они относятся к вещам, не связанным друг с другом. И наконец, можно попробовать справиться с мультиколлинеарностью, отбросив одну или
[c.451] несколько тесно связанных переменных. Это может привести к искажениям, но, убирая сначала одну, потому другую из связанных НП и сравнивая результаты регрессий, можно по меньшей мере составить представление о том, какой урон наносят искажения, а какой – мультиколли-неарность.Сравнение независимых переменных.
Всегда важно знать, какая из нескольких НП оказывает наибольшее влияние на зависимую переменную. Если бы мы хотели заставить людей, к примеру, пристегивать ремни, нам понадобилось бы, наверное, узнать, какие из факторов, способных вызвать такое поведение, могут сильнее всего повлиять на решение пристегиваться, и затем действовать наиболее эффективными методами. Анализ с применением множественной регрессии очень хорошо подходит для этого, поскольку предусматривает оценку влияния каждой отдельной НП на колебания ЗП одним из своих методов – частным коэффициентом регрессии. К сожалению, определение относительного влияния разных НП не тождественно простому сравнению их коэффициентов регрессии.В тех случаях, когда НП измеряются в разных единицах (количество долларов наряду с процентом избирателей, например), коэффициенты регрессии не отражают относительного воздействия НП на ЗП. Одним из возможных путей обойти это – стандартизировать переменные так, чтобы они были измерены в одних и тех же единицах, и снова произвести подсчеты коэффициента регрессии. Стандартизация измерений достигается путем преобразования числового ряда в единицы стандартного отклонения от значения среднего геометрического переменной посредством использования следующей формулы:
![]()
где звездочка означает, что переменная стандартизована;
X – значение данного признака;
![]() – значение среднего геометрического этой переменной для всех признаков;
– значение среднего геометрического этой переменной для всех признаков;
SX – стандартное отклонение распределения значений переменной X (см.
Когда числовые ряда заменены в уравнении регрессии на стандартизованные ряды, а выпадает, потому что стандартизация сводит его к 0, и уравнение приходит к общей формуле:
Y’ = а + β 1X1* + β 2X2* + β 3X3* +…+ β nXn* + е,
где β представляет частный коэффициент стандартизованной регрессии и называется
бета-вес, или бета-коэффициент. Вес корректирует частный нестандартизованный коэффициент регрессии путем деления стандартного отклонения НП на стандартное отклонение ЗП и может быть посчитан по формуле:
![]()
Бета-вес может быть интерпретирован как среднее изменение стандартного отклонения переменной Y,
связанное с измерением стандартного отклонения переменной Х при постоянном воздействии других НП. Таким образом, β со значением 0,5 означает, что изменение значения НП в одно стандартное отклонение вызовет изменение ЗП в половину стандартного отклонения.Таким образом, стандартизация позволяет сравнивать влияние нескольких независимых переменных внутри одного массива. Если же нам нужно выяснить взаимосвязи переменных между массивами, этот способ может ввести в заблуждение. Если, например, нам захочется изучить влияние количества вложенных средств на успех кандидатов на выборах в Соединенных Штатах и Мексике, мы обнаружим, что в распределении (а следовательно и в стандартном отклонении) ключевых переменных были существенные различия, поскольку организация кампании в средствах массовой информации в Соединенных Штатах стоит больше, и результаты выборов зависят от этого в одной стране больше, чем в другой. Поскольку значение β является функцией вариации переменных (чем больше вариация, тем больше β при прочих равных условиях), мы можем ошибаться, думая, что вложение средств дает в одной стране больший эффект, чем в другой, просто потому, что таковы математические обусловленные значения β. Чтобы избежать такой ошибки, необходимо принять во внимание частный наклон
[c.453] нестандатизованной регрессии в любом случае сравнения влияний НП в различных массивах, если вариация этой переменной значительно меняется от массива к массиву6. [c.454]ПАТ-АНАЛИЗ
*Регрессионный анализ может быть достаточно полезен для проверки отдельных гипотез и изучения относительного влияния различных независимых переменных. Однако регрессия предлагает такую модель причинных связей, которая не всегда отражает всю сложность окружающего мира. Если нам захочется определить решающие факторы расовой сегрегации в системе общеобразовательных школ, например, мы можем предположить, что школьная сегрегация вызвана сегрегацией в системе расселения (поскольку большинство школ тяготеет к географическим регионам), а она в свою очередь расовыми различиями в доходах. Диаграмма причин, или модель взаимосвязей, построенная по схеме, предложенной в
гл. 2, изображена на модели 1.Модель 1. X1
– расовые различия в доходах, Х2 – жилищная сегрегация и Х3– школьная сегрегация
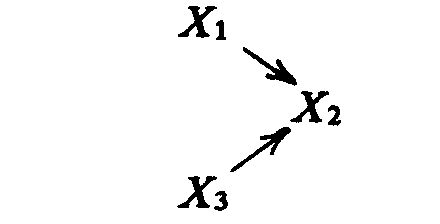
Эта простая диаграмма – типичная модель, полученная в результате обычного регрессионного анализа; она показывает, что НП оказывают воздействие на ЗП независимо друг от друга. В реальной же социальной ситуации НП часто влияют друг на друга так же, как и на ЗП. Если вспомнить наш пример, то мало-мальские знания об объекте исследования позволят предположить, что различия в доходах влияют на жилищную сегрегацию так же, как и на школьную сегрегацию, поскольку менее дорогие и более дорогие дома обычно географически тяготеют друг к другу. Признание этого факта означало бы, что мы пересмотрели нашу модель, Можно предположить, что существует последовательное развитие, в
[c.454] котором одна НП оказывает воздействие на ЗП исключительно через изменения, вызванные ею в другой НП. Это можно изобразить так:Модель 2
![]()
Более глубокое проникновение в предмет может привести к пониманию того факта, что расовые различия в доходе влияют на школьную сегрегацию как прямо, так и через жилищную сегрегацию, поскольку более состоятельные люди могут помещать своих детей в частные школы. Эту информацию можно отразить в модели путем изображения прямых стрелок от X1 к
Х3, как в модели 3.Модель 3.
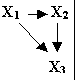
Пат-анализ – это способ статистического анализа, которым можно оценить точность таких моделей путем эмпирической оценки прямых и непрямых воздействий одной переменной на другую. Его широко применяют в социальных науках, поскольку он пригоден для решения широкого круга исследовательских задач и имеет то преимущество, что с его помощью можно проверить сразу значительную долю теории, а не проверять каждую гипотезу в отдельности. Наша цель – познакомить вас с основными процедурами пат-анализа и научить читать пат-диаграммы, которые могут встретиться вам в литературе. Мы не станем вникать во все детали, усвоение которых необходимо для более серьезного и глубокого применения этого метода, поэтому вы поступите мудро, если почитаете что-нибудь еще, прежде чем попытаетесь применить пат-анализ для решения сложных исследовательских задач.
Рекурсивные и нерекурсивные модели. Пат-анализ начинается с построения концептуальной модели, которая выделяет причинные связи, реально существующие, по мнению исследователя, в окружающем мире. Для пат-анализа модель 3 следует перестроить и представить как модель 4, где величина обозначает те колебания связанных с ними переменных, которые не могут быть объяснены колебаниями других переменных в модели. [c.455]
Модель 4
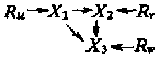
Затем модель представляется в виде математического уравнения. Однако любая модель, в которой НП независимы друг от друга (как в модели 1), не может быть представлена одним уравнением, ее следует описывать несколькими структурными уравнениями. Модель 4 будет представлена следующим набором уравнений:
X1 = р1uRu;
Х2 = p21X1 +p2vRv;
Х3 = p32X2 + p31X1b+ p3wRw.
p в этих уравнениях представляет пат-коэффициенты, которые подытоживают размер или силу воздействия, оказываемого одной переменной на другую при постоянных воздействиях других переменных. Общепринятый способ написания пат-коэффициента – pij, что обозначает направление от переменной j к переменной i. Таким образом, набор данных уравнений говорит о том, что величина X1 целиком обусловлена факторами, лежащими за пределами модели, величина X2 обусловлена X1 и факторами вне модели, и величина X3 обусловлена X1, X2 и факторами вне модели. Такие переменные, как X2 и X3, которые хотя бы частично определены другими переменными данной модели, называются эндогенными, а переменные, полностью обусловленные внешними по отношению к модели факторами, называются экзогенными.
Модели подразделяются на рекурсивные и нерекурсивные. Модель рекурсивна тогда, когда все задействованные в ней переменные могут быть расположены так, что первая будет определяться только внешними факторами, вторая – только внешними факторами и первой переменной, третья – только внешними факторами и первой и второй переменными и т.д. Короче говоря, все это означает, что все причинные влияния должны осуществляться в одном направлении без “обратной связи”7. Модель 4 – это пример рекурсивной модели.
Если между любыми переменными модели существует обратная связь (взаимная причинность), то она считается [c.456] нерекурсивной. Например, мы могли добавить переменную “род занятий” (X4) к модели школьной сегрегации и заявить, что раздельное обучение ведет к расовым различиям в профессиональных достижениях, а это в свою очередь вызывает различия в доходах, так что модель уже будет выглядеть как модель 5.
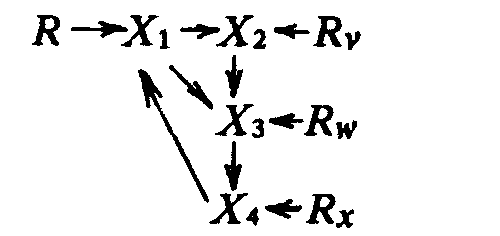
Модель 5. Эта модель уже не содержит переменных, целиком обусловленных внешними по отношению к ней факторами, и является нерекурсивной. Такие модели требуют особых способов анализа, что лежит за рамками данной книги8. Впрочем, рекурсивные модели вполне можно изучать методами обычной регрессии наименьших квадратов, описанной выше. Если переменные представлены в стандартизованном виде, пат-коэффициенты можно посчитать, как коэффициенты стандартизованной регрессии, производные от регрессии.
Использование пат-анализа. Можно проверить эмпирические предположения насчет верности выдвинутых в модели предположений путем подсчета серии регрессий, где каждая эндогенная переменная регрессировала со всеми переменными, которые предположительно на нее влияют. Чтобы пример был чисто гипотетический, возьмем пятипеременную рекурсивную модель, изображенную на модели 6 (остаточное влияние убрано для простоты изображения).
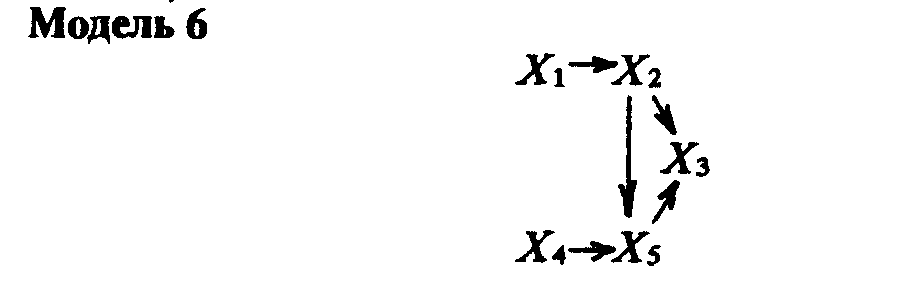
Чтобы проверить эту модель, мы определим регрессию X5 на X1 через X4, Х4 на X2 и X3 и X3 на X1. X1 и X3 будем считать экзогенными. Если значение любого из пат-коэффициентов (коэффициентов стандартизованной
[c.457] регрессии), полученных при этих расчетах, приближается к 0 или является статистически незначимым, то это свидетельствует о том, что мы неверно построили модель, предположив в ней взаимосвязь, которой на самом деле в данных нет.Кроме этого, можно проверить верность наших предположений относительно отсутствия взаимодействия путем вычисления регрессии между эндогенными переменными и теми, с которыми они, по нашему мнению, не связаны. Например, для проверки модели 6 нам нужно вычислить регрессию X3 на X1 и X4 на X1, чтобы выяснить, не следовало ли изобразить те стрелки, которые мы опустили. Если полученные пат-коэффициенты существенно отличны от 0 (>=0,2, например) и статистически значимы, нам придется заключить, что модель (и наша теория о тех явлениях, которые ею представлены) нуждается в пересмотре.
Одним из важнейших достоинств пат-анализа является то, что он облегчает разработку теории тем, что побуждает использовать теорию и анализ данных в плодотворном взаимодействии, где одно дополняет другое. Пат-анализ такого типа позволит судить не только о том, связаны ли переменные в нашей модели именно так, как мы предполагали, но и о том, каково относительное влияние каждой переменной на другие переменные в данной модели. Суммарное воздействие одной переменной на другую равно значению или силе прямой связи между ними плюс значение или сила непрямых связей, существующих между ними. Сила непрямой связи измеряется произведением тех прямых связей, из которых она состоит. Например, в модели 6 общее воздействие X2 на X5 равно
р52+(р42 • р54),
а общее воздействие X1 на X5 будет равно (p21 • p52) + (p21•р42• p54).
Везде, где используются коэффициенты стандартизованной регрессии, можно использовать этот способ сравнения суммарных воздействий разных переменных в рамках одной системы. Знать его крайне полезно, поскольку он может помочь как рядовым гражданам, так и руководителям направить свои усилия именно туда, где
[c.458] они будут иметь наибольший эффект. Например, если мы пытаемся убедить людей в необходимости пристегивать ремни, мы можем сначала выяснить, какой из нескольких факторов, определяющих это решение, имеет наибольшее влияние, и затем направить все усилия на изменение именно этой переменной.Пат-анализ может быть также использован для сравнения воздействия переменных в разных системах. Если вернуться к примеру о школьной сегрегации, то можно собрать данные по Антланте, Лос-Анджелесу и Детройту и проверить верность модели 4 по каждому городу. Если мы не стандартизируем данные и используем коэффициенты нестандартизованной регрессии, то мы можем сравнить, скажем, влияние жилищной сегрегации на школьную сегрегацию в каждом из этих городов, чтобы понять, как интересующие нас причинные взаимодействия изменяются от города к городу. Необходимо использовать нестандартизованные коэффициенты, поскольку стандартизация ставит значение пат-коэффициента в зависимость от вариации переменной в данном массиве. Если, например, в одном городе школьная сегрегация проявляется гораздо сильнее, чем в другом, относительный размер коэффициента стандартизованной регрессии будет отражать степень этих различий в разбросе, а не действительную разницу в относительной силе проявления этой переменной в различных городах.
Общее правило – использовать стандартизованные коэффициенты при сравнении воздействий разных переменных в рамках одного массива и нестандартизованные коэффициенты при сравнении воздействий одних и тех же переменных в различных массивах9. Считается, что именно нестандартизованные коэффициенты позволяют судить о тех “причинных законах”, которые управляют общественным развитием.
[c.459]Многие важные социальные и политические события иногда повторяются, а не случаются лишь единожды, а социальные и политические процессы порой тянутся на протяжении нескольких лет. В результате исследователям часто приходится изучать взаимодействия объектов, разделенных во времени. Средством для этого является [c.459]
анализ временных рядов. Он используется, когда нужно объяснить, что случилось в прошлом или прогнозировать события в будущем. Способы применения временных рядов сложны и требуют основательной подготовки. Они, однако, подходят для решения настолько большого круга исследовательских задач и так часто используются в разработках важных проблем, что даже начинающие должны иметь некоторое представление об их основных принципах.Временные ряды – это просто комплекс наблюдений, в которых одна и та же переменная измеряется повторно через определенные интервалы. Государственное агентство занятости может обнародовать цифры по уровню безработицы каждый месяц, международная организация может публиковать ежегодные отчеты об общем объеме международной торговли, маклерская контора может фиксировать индекс Доу-Джонса каждый день. Такие данные можно анализировать методами, основанными на тех принципах регрессии, которые обсуждались ранее. Мы начнем с обсуждения общих подходов к временным рядам и затем рассмотрим два варианта.
Регрессия временных рядов. Исследователям часто бывает необходимо объяснить наблюдаемые тренды (их еще называют секулярными трендами).
Они хотят знать, почему нечто увеличивается или уменьшается, почему оно возрастает или убывает постоянно или циклически и т.д. Например, нам нужно выяснить, насколько послевоенный (имеется в виду вторая мировая война) рост расходов на вооружения в Соединенных Штатах являлся следствием военных расходов в СССР; для этого мы строим простейшую регрессионную модель:
Y = a + bXt + et,
где Y представляет данные по военным расходам США в виде временных рядов;
а – средний уровень расходов в Соединенных Штатах;
b – влияние расходов в СССР на расходы в США;
Xt – данные по военным расходам СССР в виде временных рядов;
et – погрешность, отражающая случайные влияния на расходы в США.
Можно использовать обычную регрессию наименьших квадратов для подсчета коэффициентов в этой модели и
[c.460] попытаться объявить или предположить расходы США следствием расходов СССР. Однако для того, чтобы в результате этих подсчетов получить неотклоненные или точные значения коэффициентов, погрешности, соответствующие различным временным точкам, не должны коррелировать, как уже упоминалось при перечислении условий, лежащих в основе регрессионного анализа. Фактически внешние факторы, влияющие на размер расходов США в одной временной точке, вероятно, будут влиять и в другой. Если, к примеру, перспективы заключения контракта заставили Пентагон вложить средства в дорогое оружие абсолютно помимо каких-либо действий с советской стороны, то такое воздействие скорее всего будет сохраняться из года в год; точно так же, если члены конгресса пытаются сохранить в своих военных округах военные контракты и оборудование, их влияние на уровень расходов будет постоянно проявляться. Эти влияния в модели отражены погрешностью. И в результате эти погрешности с течением времени сильно коррелируют.Эта автокорреляция (ее еще называют серийной корреляцией) нарушает одно из условий регрессионного анализа и может привести к тому, что отклонения коэффициента а и 6 при компьютерной обработке могут быть значительно недооценены. В результате статистическая значимость этих коэффициентов будет сильно вздута, и это может привести нас к мысли, что существует взаимосвязь там, где ее на самом деле нет. По этой причине очень важно проводить тест на наличие автокорреляции и, если таковая присутствует, принять меры к устранению ее воздействия, прежде чем делать какие = либо выводы по моделям, содержащим временные ряды. Существует целый ряд статистических тестов на автокорреляцию и несколько способов ее корректировки10.
Построение временных лагов.
Часто обнаруживается, что одно событие влияет на другое только по прошествии некоторого времени. В нашем примере, скажем, маловероятно, что советские военные расходы за один год повлияют на расходы США в тот же год, поскольку уровень расходов планируется заранее и уровень советских военных расходов может быть неизвестен в момент принятия решения о расходах США. Следовательно, иногда необходимо учесть в модели, изображающей влияние одной [c.461] переменной на другую, временной лаг. На простейшем уровне мы можем сделать это, сравнивая расходы США с расходами СССР за предыдущий год. Наша основная модель, таким образом, будет выглядеть вот так:Yt = a + bXt–1 + et,
где t–1 означает запаздывание в один год.
Прерванные временные ряды. Часто исследователю бывает необходимо определить влияние единичного события на поведение переменной. Например, можно попытаться измерить влияние принятия закона о необходимости пристегивать автомобильные ремни на количество смертельных исходов в автокатастрофах в определенной стране. Для этого нужно собрать данные о количестве смертельных случаев, отмеченных за каждый месяц в течение нескольких лет до принятия закона и нескольких лет после (может быть, следует фиксировать количество смертей в процентах от общего количества людей, вовлеченных в автокатастрофы за месяц, с тем чтобы обеспечить реальную почву для сравнения периодов, в течение которых количество происшествий сильно менялось). Обнаружится, однако, что выяснить влияние закона простым сравнением количества смертей до закона и после его принятия довольно сложно, поскольку мы сравниваем не единичное измерение, а комплекс измерений. Значения могут существенно изменяться как до, так и после принятия закона, так что визуальное изучение данных не даст очевидного результата.
Значения переменных в любых временных рядах могут изменяться по трем основным причинам: (1) секулярные тренды (долговременные тенденции к увеличению или уменьшению); (2) циклические отклонения или сезонность (тенденции к регулярному росту или падению в течение длительного времени) и (3) случайные отклонения (изменения, являющиеся следствием единичных событий, как, например, неожиданная метель для нашего случая, или ошибок в измерении переменной, как, например, случайное отнесение телесных повреждений к числу смертных случаев). Прежде чем мы сможем определить влияние любого конкретного события на временной ряд, необходимо исключить изменения, являющиеся следствием
[c.462] трендов, сезонных и случайных факторов. Кроме того, важно осознать, что в любом временном ряду такого типа, вероятно, возникнут серьезные проблемы, связанные с автокорреляцией, поскольку погрешности в разных наблюдениях обычно сильно коррелируют, делая невозможным точный подсчет коэффициентов.К счастью, в статистике разработан способ, с помощью которого можно приспособить регрессионный анализ к такой ситуации. Этот способ называется авторегрессивные интегрированные движущиеся средние модели (АРИМА – аббревиатура английского названия), они приспособлены к факторным трендам, сезонности и случайным воздействиям извне временных рядов и одновременно к автокорреляции так, что истинное влияние помех ясно видно11. Хотя мы здесь не располагаем достаточным местом, чтобы объяснить, как работают эти методики, исследователям следует знать об их существовании, поскольку они делают возможным использование прерванных временных рядов как форму квазиэксперимента, где вызывающие помехи события (революция, стихийное бедствие, расследование коррупции в государственном учреждении, введение новой технологии и т. д.) рассматриваются как стимул или НП, а значения ЗП выполняют функции контрольной группы12. Такие исследования могут позволить нам сделать некоторые ценные выводы относительно тех причин важных событий, которые не были предусмотрены при постановке задач исследования, и, следовательно, открыть путь к решению целого ряда исследовательских задач, которые иначе могли бы остаться вне сферы нашего внимания.
[c.463]Мы закончим эту главу двумя оговорками. Во-первых, необходимо понимать, что мы обсудили лишь некоторые из многочисленных многомерных статистик, позволяющих анализировать как интервальные, так и неинтервальные данные. Каждая из этих методик приложима к решению различных аналитических задач. Среди наиболее распространенных методик, которые мы не обсудили здесь, следует упомянуть такие, как: дискриминантный анализ, определяющий статистически значимые различия в дихотомических группах и, таким образом, наилучшим
[c.463] образом подходящий для экспериментальных и квазиэкспериментальных работ; анализ вариаций, который используется для проверки гипотез об отличиях средних геометрических в различных группах и может оказаться особенно полезным в определении влияний некоторых “воздействий” или помех на то, как отдельные случаи укладываются в концепцию; факторный анализ, который используется для определения тех факторов, которые отражают наличие связей между кажущимися независимыми переменными. Объяснения того, когда и как можно использовать эти и другие методики, можно найти в списке дополнительной литературы в конце этой главы.Второе, о чем хотелось бы сказать, – это то, что вышеизложенное на самом деле не подготовит вас к выполнению сложных видов статистического анализа. К счастью, не нужно быть статистиком, для того чтобы использовать наиболее важные методы, поскольку программы статистического анализа как для микро-, так и для персонального компьютера и ЭВМ выполнят для вас все подсчеты, если, конечно, вы знаете, как верно построить анализ. Большинство этих программ имеет хорошо скомпонованные инструктирующие учебники-самоучители, которые помогут разобраться в статистических процедурах и в необходимом программировании. Таким образом, нелюбовь к математике или статистике не должна стать непреодолимым препятствием для относительно сложных видов анализа данных и эмпирических исследований важных политических тем.
[c.464]
По статистике существует великое множество доступных книг. Войти в курс дела вам помогут кн.: Мооre D.S. Statistics, 3d ed. – N.Y.: Freeman, 1991. Соuсh J.V. Fundamentals of Statistics for the Behavioral Sciences. – N.Y.: St. Martin Press, 1982; Bohrnstedt G.W., Knoke D. Statistics for Social Data Analysis. – Itasca (Ill.): F.E. Peacock, 1982; Tabachnick B.G., Fidell L.S. Using Multivariate Statistics. – N.Y.: Harper and Row, 1983. Более углубленное изучение статистических приемов содержится в кн.: Касhigan S.K. Multivariate Statistical Analysis. N.Y.: Radius Press, 1982; Lindeman R., Merenda P.P., Gold R.Z. Introduction to Bivariate Multivariate Analysis. – Dallas: Scott Foresman, 1980.
Методы анализа неинтервальных данных детально рассмотрены в кн.: Gibbons J.D. Nonparamctric Statistical Inference. – N.Y.: McGraw-Hill; 1971; Heise D.R. Causal Analysis. – N.Y.: Wiley, 1975. Книга Гиббонса дает прекрасное представление о пат-анализе. О многих статистических методах дают представление книги серии: Quantitative Applications in the Social Science. В большинстве этих книг даны конкретные примеры применения методик, которые в них описаны. См. также о применении статистики: Hubert M., Blalock H.M„ Jr. ed. Causal Models in the Social Sciences. – N.Y.: Aldine, 1985, 2nd. ed. В книге основное внимание уделено пат-анализу; Rhodes T.L, Аrringtоn Th.S., Мundt R. Applied Political Inquiry. – N.Y.: University Press of America, 1982; McCleary R., Hay R.A. Applied Time-Series Analysis for the Social Sciences. – Beverly Hills, Calif.: Sage, 1980.
[c.465]
1
Для уяснения логики такого анализа см.: Bohrnstedt Y.W., Кnоke D. Statistics for Social Data Analysis. – Itaska (Ill.): F.F.Peacock, 1982, chap. 10.
2
Для уяснения этих условий и более глубокого понимания множественной регрессии см.: Pedhazur E.J. Multiple Regression in Behavioral Research. – N.Y.: Holt, Rinehart and Winston, 1982, 2d ed.
3
Исследования редко удовлетворяют этим условиям полностью, и часто до проведения анализа нельзя сказать, удовлетворяет ли им конкретных набор данных. Исходя из этого, “достаточно полно” значит, что действие любого отклонения от этих условий может быть скорректировано или по меньшей мере подсчитано. См.: Pedhazur, op. cit.
4 По поводу расчетов значимости в регрессивном анализе см.: Касhigan S.K. Multivariate Statistical Analysis. – N.Y.: Radius Press, 1982, pp. 178-179.
5
Подробнее см.: Lewis–Beck M.S. Applied Regression. – Beverly Hills (Calif.): Sage, 1980, pp. 66-71.
6
Некоторые предостережения насчет этого правила и предложения о том, как сравнивать влияния различных переменных между массивами содержатся в кн.: Hotchkiss L. A Technique for Comparing Path Models Between Subgroups Standardized Path Coefficients. – Regression Coefficients. // Sociological Methods and Research. – 1976 (August). – Vol. 5. – P. 53-76.
* От англ. path – путь, траектория
7
Другие требования к рекурсивным моделям обсуждаются в кн.: Dunсаn O.D. Introduction to Structural Equation Models. – N.Y.: Academic Press, 1975.
8 О методах анализа с обратной связью см.: Berry W.D. Nonrecursive Casual Models. – Beveriy Hills (Calif.): Sage, 1984.
9
См.: Асhen Ch.H. Interpreting and Using Regression. – Beverly Hills (Calif.): Sage, 1992.
10
Эта тема хорошо раскрыта в кн.: Оstгоm Сh. W. Time Series Analysis. Beverly Hills (Calif.): Sage, 1978.
11
Добротное описание принципов и использования РИМА см. в кн.: Cook D.Th., Campbell D.T. Ouasiexperimentation. – Chicago: Rand McNally, 1979, chap. 6.
12
См.: Cook, Campbell, chap. 5.