 |
 |
|
ПОЛИТОЛОГИЯ: МЕТОДЫ ИССЛЕДОВАНИЯ |
|
НАЗАД Мангейм Дж., Рич Р.К. Политология. Методы исследования ВПЕРЕД
Красным шрифтом в квадратных скобках обозначается конец текста на соответствующей странице печатного оригинала данного издания
5. КТО, ЧТО, ГДЕ, КОГДА: ПРОБЛЕМА ВЫБОРКИ
Раз в десять лет Бюро переписи, отдел министерства торговли США, проводит перепись, стремясь определить, подсчитать и измерить определенные характеристики образа жизни каждого человека в стране. Закон требует, чтобы все сотрудничали с лицами, проводящими перепись, и давали правдивые ответы на вопросы типа: “сколько у вас телевизоров?”, “есть ли в вашем доме водопровод?”. По имеющимся оценкам, перепись 1990 г. обошлась федеральному правительству в 2 600 000 000 долларов; для получения соответствующей информации было привлечено 480000 служащих, интервьюеров и других лиц, работавших в течение нескольких месяцев. Всего в США было идентифицировано и обследовано около 250 000 000 человек.
Надо ли говорить, что не многие политологи готовы к таким огромным затратам для удовлетворения своих личных исследовательских интересов. В то же время объекты их интересов (объекты исследования) для различных практических целей могут быть столь же многочисленны. Сто миллионов избирателей, четверть миллиарда жителей западных демократий, сто тысяч документов – все это может оказаться в центре внимания политологического исследования, хотя количество отдельных объектов в каждом из этих случаев слишком велико, чтобы их можно было всесторонне проанализировать. Даже Бюро переписи, со всеми его тысячами работников и миллионами долларов, оказалось не в состоянии задать каждому идентифицированному липу все свои вопросы. Вместо этого была разработана короткая анкета для большинства населения и более полная для отдельных респондентов. Так же как политологи и многие другие исследователи, Бюро переписи сочло необходимым использовать выборку.
В настоящей главе мы рассмотрим применение и механизм формирования выборки, отбора сравнительно небольшого числа объектов, изучение которых может дать
[c.153] нам большой объем информации о генеральной совокупности, из которой они были выбраны. Поступая таким образом, мы будем иметь дело с тем, что мы назвали генерализацией, возможностью делать общие выводы, основанные на анализе небольшого числа объектов. С этой целью мы должны задать себе три вопроса. Во-первых, что же такое репрезентативная выборка? Во-вторых, какие существуют возможности для отбора конкретных объектов, которые образовали бы такую выборку? И в-третьих, сколько объектов необходимо отобрать, чтобы можно было назвать выборку репрезентативной? Рассмотрим поочередно все эти вопросы. [c.154]Фактически мы начнем не с одного, а с трех вопросов: что такое выборка? когда она является репрезентативной? что она собой представляет?
Совокупность – это любая группа людей, организаций, интересующих нас событий, относительно которых мы хотим сделать выводы, а случай, или объект, – любой элемент такой совокупности1. Выборка – любая подгруппа совокупности случаев (объектов), выделенная для анализа. Если мы захотим изучить деятельность законодателей штата по принятию решений, мы могли бы исследовать такую деятельность в законодательных органах штатов Виргиния, Северная Каролина и Южная Каролина, а не во всех пятидесяти штатах и, исходя из этого, распространить полученные данные на генеральную совокупность, из которой были выбраны эти три штата. Если мы хотим исследовать систему предпочтений избирателей Пенсильвании, мы могли бы сделать это, опросив 50 рабочих компании “Ю. С. Стил” в Питсбурге, и распространить результаты опроса на всех избирателей штата. Аналогично, если мы хотим измерить умственные способности студентов колледжей, мы могли бы протестировать всех игроков защиты, зарегистрированных в штате Огайо в данном футбольном сезоне, и затем распространить полученные результаты на генеральную совокупность, частью которой они являются. В каждом примере мы действуем следующим образом: устанавливаем подгруппу внутри генеральной совокупности, довольно [c.154] подробно изучаем эту подгруппу, или выборку, и распространяем наши результаты на всю совокупность. Это и есть основные этапы формирования выборки.
Однако представляется совершенно очевидным, что каждая из этих выборок имеет существенный недостаток. К примеру, хотя законодательные органы Виргинии, Северной Каролины и Южной Каролины и являются частью совокупности законодательных органов штатов, они в силу исторических, географических и политических причин, скорее всего, будут действовать очень схожим образом и совсем иначе, чем законодательные органы таких отличающихся от них штатов, как Нью-Йорк, Небраска и Аляска. Хотя пятьдесят рабочих-сталелитейщиков в Питсбурге действительно могут быть избирателями штата Пенсильвания, они в силу социально-экономического статуса, образования и жизненного опыта, вполне возможно, будут иметь взгляды, отличные от взглядов многих других людей, точно так же являющихся избирателями. И точно так же, хотя футболисты штата Огайо и являются студентами колледжей, они в силу самых разных причин вполне могут отличаться от других студентов. Иными словами, хотя каждая из этих подгрупп действительно является выборкой, члены каждой из них систематически отличаются от большинства остальных членов совокупности, из которой они выбраны. В качестве отдельной группы ни одна из них не является типичной с точки зрения распределения признаков мнений, мотивов поведения и характеристик в генеральной совокупности, с которой она ассоциируется. Соответственно, политологи сказали бы, что ни одна из этих выборок не является репрезентативной.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности. Таким образом, если 50% всех законодательных органов штатов собираются лишь раз в два года, приблизительно половина состава репрезентативной выборки законодательных органов штатов должна быть такого типа. Если 30% избирателей Пенсильвании принадлежат к “синим воротничкам”, около 30% репрезентативной [c.155] выборки для этих избирателей (а не 100%, как в приведенном выше примере) должны быть из числа “синих воротничков”. И если 2% всех студентов колледжей являются спортсменами, приблизительно та же самая часть репрезентативной выборки студентов колледжей должна приходиться на спортсменов. Иными словами, репрезентативная выборка представляет собой микрокосм, меньшую по размеру, но точную модель генеральной совокупности, которую она должна отражать. В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выборки, можно без всяких опасений считать применимыми к исходной совокупности. Это распространение результатов и есть то, что мы называем генерализуемостью.
Возможно, пояснить это поможет графическая иллюстрация. Предположим, мы хотим изучать модели членства в политических группах среди взрослого населения США. На рис.5.1 изображено три круга, разделенных на шесть равных секторов. Рис.5.1а представляет всю рассматриваемую совокупность. Члены совокупности расклассифицированы в соответствии с политическими группами (такими, как партии и группы интересов), к которым они относятся. В этом примере каждый взрослый принадлежит по меньшей мере к одной и не более чем к шести политическим группам; и эти шесть уровней членства в одинаковой степени распространены в совокупности (отсюда равные сектора). Предположим, мы хотим исследовать мотивы вступления людей в группу, выбор группы и модели участия, однако из-за ограниченности ресурсов мы в состоянии обследовать только одного из каждых шести членов совокупности. Кого же отобрать для анализа?
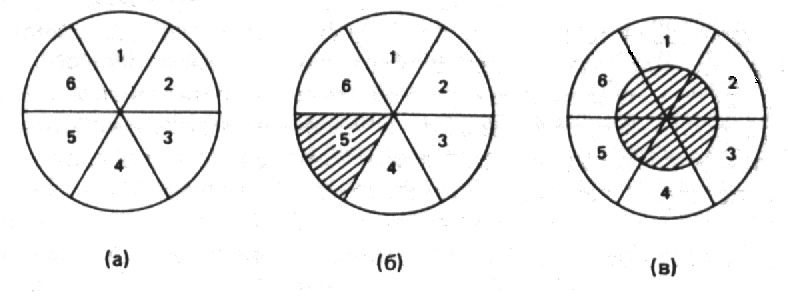
Рис. 5.1. Формирование выборки из генеральной совокупности
Одну из возможных выборок заданного объема иллюстрирует заштрихованная область на рис.5.1б, однако она явно не отражает структуру совокупности. Если бы мы делали обобщения на основе этой выборки, мы пришли бы к выводу: (1) что все взрослые американцы принадлежат к пяти политическим группам и (2) что все групповое поведение американцев совпадает с поведением тех, кто принадлежит именно к пяти группам. Однако мы знаем, что первый вывод не верен, и это может зародить в нас сомнение относительно валидности второго. Таким образом,
[c.156] выборка, изображенная на рис.5.1б, нерепрезентативна, поскольку она не отражает распределение данного свойства совокупности (часто называемого параметром) в соответствии с его реальным распространением. Про такую выборку говорят, что она смещена в направлении к членам пяти групп или смещена в направлении от всех остальных моделей членства в группах. Опираясь на такую смещенную выборку, мы обычно приходим к ошибочным выводам относительно генеральной совокупности.Ярче всего это может быть продемонстрировано на примере катастрофы, постигшей в 30-е годы журнал “Литэрари дайджест”, который организовал опрос общественного мнения относительно результатов выборов. “Литэрари дайджест” представлял собой периодическое издание, в котором перепечатывались редакционные статьи из газет и другие материалы, отражавшие общественное мнение; этот журнал был очень популярен в начале века. Начиная с 1920 г. журнал проводил широкомасштабный общенациональный опрос, в ходе которого более чем миллиону человек по почте рассылались избирательные бюллетени с просьбой отметить, чья кандидатура на предстоящих президентских выборах для них предпочтительнее. В течение ряда лет результаты опроса, проводившиеся журналом, оказывались настолько точными, что опрос, проведенный в сентябре, казалось, делал ноябрьские выборы малосущественными. Да и как при такой большой выборке могла произойти ошибка? Однако в 1936 г. именно это и случилось: с большим перевесом голосов (60:40) победа была предсказана кандидату от республиканской партии Альфу Ландону. На выборах Ландон проиграл инвалиду –
[c.157] Франклину Д. Рузвельту – практически с тем же результатом, с которым должен был победить. Доверие к “Литэрари дайджест” было столь сильно подорвано, что вскоре после этого журнал перестал выходить. Что же произошло? Все очень просто: в голосовании, проведенном “Дайджест”, использовалась смещенная выборка. Почтовые открытки рассылались людям, чьи имена были извлечены из двух источников: телефонных справочников и списков регистрации автомобилей. И хотя прежде этот метод отбора не слишком отличался от других методов, совсем по-другому обстояло дело теперь, во время Великой депрессии 1936 г., когда менее состоятельные избиратели, наиболее вероятная опора Рузвельта, не могли позволить себе иметь телефон, не говоря уж об автомобиле. Таким образом, фактически выборка, использовавшаяся в опросе, организованном “Дайджест”, была смещена в сторону тех, кто, скорее всего, должен был выступать за республиканцев, и при этом еще удивительно, что у Рузвельта был такой хороший результат.Как же решить эту проблему? Возвращаясь к нашему примеру, сравним выборку на рис.5.1б с выборкой на рис.5.1в. В последнем случае для анализа также отобрана шестая часть совокупности, однако каждый из основных типов совокупности представлен в выборке в той пропорции, в которой он представлен во всей совокупности. Такая выборка демонстрирует, что один из каждых шести взрослых американцев принадлежит к одной политической группе, один из шести – к двум и т.д. Такая выборка позволит также выявить другие различия между ее членами, которые могли бы соотноситься с участием в разном числе групп. Таким образом, выборка, представленная на рис.5.1в, является репрезентативной выборкой для рассматриваемой совокупности.
Конечно, данный пример является упрощенным по крайней мере с двух чрезвычайно важных точек зрения. Во-первых, большинство совокупностей, интересующих политологов, более разнообразно, чем та, что приведена в примере. Люди, документы, правительства, организации, решения и т.п. отличаются друг от друга не по одному, а по гораздо большему числу признаков. Таким образом, репрезентативная выборка должна быть такой, чтобы каждая из основных, отличная от других область была
[c.158] представлена пропорционально ее доле в совокупности. Во-вторых, ситуация, когда реальное распределение переменных, или признаков, которые мы хотим измерить, заранее неизвестно, встречается гораздо чаще, чем противоположная, – возможно, оно не измерялось в предшествующей переписи населения. Таким образом, репрезентативная выборка должна быть построена так, чтобы она могла точно отражать существующее распределение даже тогда, когда мы не в состоянии прямо оценить ее валидность. Процедура формирования выборки должна иметь внутреннюю логику, способную убедить нас, что, будь мы в состоянии сравнить выборку с переписью, она действительно оказалась бы репрезентативной.Чтобы обеспечить возможность точного отражения сложной организации данной совокупности и определенную степень уверенности в том, что предлагаемые процедуры способны сделать это, исследователи обращаются к методам статистики. При этом они действуют по двум направлениям. Во-первых, используя определенные правила (внутреннюю логику), исследователи решают вопрос о том, какие именно конкретные объекты им изучать, что именно включать в конкретную выборку. Во-вторых, используя совсем другие правила, они решают, сколько объектов выбрать. Мы не будем подробно изучать эти многочисленные правила, рассмотрим лишь их роль в политологическом исследовании. Начнем рассмотрение со стратегий выбора объектов, образующих репрезентативную выборку.
[c.159]ПРОЦЕДУРЫ ФОРМИРОВАНИЯ РЕПРЕЗЕНТАТИВНОЙ ВЫБОРКИ
Как видно из примеров предыдущего раздела, не все выборки в равной степени репрезентативны. Действительно, фиаско, постигшее “Литэрари дайджест”, хотя и один из самых известных, однако вряд ли единственный пример исследования, опиравшегося на плохо сформированную выборку. Предварительные выборы, в которых люди участвуют по собственной воле и могут голосовать за кандидата более одного раза; уличные интервью, в которых выбор места и невозможность контроля за прохожими могут оказать сильное воздействие на результаты; результаты проводимых законодателями опросов в большой
[c.159] степени зависят от взглядов более красноречивого и интересующегося политикой меньшинства, представители которого, скорее всего, и будут отвечать на заданные вопросы; анализ иностранной прессы, пропагандистских материалов или материалов, опубликованных исключительно в англоязычных источниках, которые могут почему-либо отличаться от других источников того же самого типа, а также слепое формирование выборки, когда исследователь просто оставляет в определенном месте пачку анкет с инструкциями по их заполнению и отказывается от всякого контроля за отбором респондентов (подход, особенно характерный для студентов-дипломников), – все это типичные примеры смещения выборки. Частично эти трудности можно разрешить с помощью осторожного (и очень строго ограниченного) определения совокупности, на которую мы собираемся распространить наши выводы. В случае уличных интервью, например, мы могли бы пожелать распространить полученные результаты лишь на тех людей, которые проходят в данном месте между 10.00 и 11.15 утра 4 марта. Однако с гораздо большим успехом имеющиеся трудности можно разрешить, лишь разработав систематическую и гораздо более изощренную процедуру отбора объектов для анализа.Ведущий принцип, лежащий в основе такой процедуры, – это принцип рандомизации, случайности. Выборка называется
случайной (иногда мы будем говорить простая случайная или чистая случайная выборка), если выполняется два условия. Во-первых, выборка должна быть построена таким образом, чтобы любой человек или объект в пределах совокупности имел равные возможности быть отобранным для анализа. Во-вторых, выборка должна быть сформирована так, чтобы любое сочетание из п объектов (где п – просто количество объектов, или случаев, в выборке) имело равные возможности быть отобранным для анализа. Все это звучит довольно сложно. И действительно, это более строгое определение случайности, чем то, которым мы пользуемся в быту; однако в основе своей случайный выбор – довольно простое и незамысловатое понятие. Это почти то же самое, что выбор с помощью лотереи. Если у нас имеется совокупность, состоящая из 1000 человек, чье поведение мы хотим изучить, исследовав репрезентативную выборку, состоящую из [c.160] 100 человек, мы могли бы написать имена всех 1000 членов совокупности на листочках бумаги одинакового размера, сложить их в барабан, хорошо перемешать и отобрать имена 100 человек в нашу в выборку. При такой процедуре каждый человек имеет равную вероятность быть выбранным (100 шансов из 1 000, или, иными словами, 1 шанс из 10), любое возможное сочетание из 100 человек также имеет равную вероятность выбора. Наличие этих двух видов равновероятности и делает выборку случайной.При исследовании совокупностей, которые слишком велики, для того чтобы можно было осуществить настоящую лотерею, часто используются простые случайные выборки. Выписать имена нескольких сотен тысяч объектов, сложить их в барабан и выбрать несколько тысяч – это все же нелегкая работа. В таких случаях используется другой, однако столь же надежный способ. Каждому объекту в совокупности присваивается номер. Номера объектов, которые будут включены в выборку, определяются с помощью
таблицы случайных чисел типа табл. A.1 в приложении А, фрагмент которой воспроизведен на рис.5.2. Последовательность чисел в таких таблицах обычно задается компьютерной программой, называемой генераторам случайных чисел, который, в сущности, помещает в барабан большое количество чисел, случайным образом вытаскивает их и выпечатывает в порядке получения. Иными словами, имеет место все тот же процесс, характерный для лотереи, однако компьютер, используя не имена, а числа, осуществляет универсальный выбор. Этим выбором можно пользоваться, просто присвоив каждому из наших объектов номер.
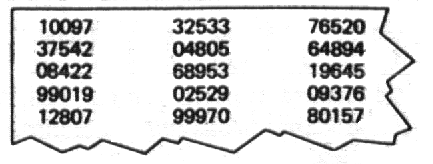
Рис. 5.2. Фрагмент таблицы случайных чисел
Таблица случайных чисел типа той, что представлена на рис.5.2, может использоваться несколькими разными способами, и в каждом случае необходимо принять три решения. Во-первых, следует решить, сколько разрядов мы будем использовать, во-вторых, необходимо разработать [c.161] решающее правило для их использования; в-третьих, нужно выбрать исходную точку и способ прохождения по таблице.
Первое решение определяется просто количеством объектов в совокупности. Если совокупность состоит из менее чем 10 объектов, используются однозначные числа; при числе объектов от 10 до 99 – двузначные числа; от 100 до 999 – трехзначные и т.д. В каждом случае мы должны позаботиться о том, чтобы каждый перенумерованный объект имел возможность быть выбранным.
Как только это сделано, мы должны разработать правило, которое бы связывало числа в таблице с номерами наших объектов. Здесь существуют две возможности. Самый простой способ (хотя и не обязательно самый правильный) – использовать лишь те числа, которые попадают в число номеров, приписанных нашим объектам. Так, если мы имеем совокупность, состоящую из 250 объектов (и, таким образом, используем трехзначные числа), и решаем начать с левого верхнего угла таблицы и двигаться вниз по столбцам, мы включим в нашу выборку объекты с номерами 100, 084 и 128 и пропустим числа 375 и 990, не соответствующие нашим объектам. Этот процесс будет продолжаться до тех пор, пока не будет определено число объектов, нужных для нашей выборки.
Более трудоемкая, однако методически более правильная процедура основывается на положении, что для сохранения случайности, характерной для таблицы, должно быть использовано каждое число данной размерности (например, каждое трехзначное число). Следуя данной логике и вновь имея дело с совокупностью из 250 объектов, мы должны разбить область трехзначных чисел от 000 до 999 на 250 одинаковых промежутков. Поскольку таких чисел 1000, мы делим 1000 на 250 и находим, что каждая из частей содержит четыре числа. Таким образом, числа таблицы от 000 до 003 будут соответствовать объекту 1, от 004 до 007 – объекту 2 и т.д. Теперь, чтобы установить, какой номер объекта соответствует числу таблицы, следует разделить трехзначное число из таблицы и округлить до ближайшего целого числа. С помощью данного метода тот же фрагмент таблицы, которым мы пользовались раньше, позволит нам включить в выборку объекты 025 (100:4), 093 (375:4, округлено в меньшую сторону), [c.162] 021 (084:4), 247 (990:4, округлено в меньшую сторону) и 032 (128:4) и не пропустить ни одного числа из таблицы.
И наконец, мы должны выбрать в таблице исходную точку и способ прохождения. Исходной точкой может быть верхний левый угол (как в предыдущем примере), нижний правый угол, левый край второй строки или любое другое место. Этот выбор абсолютно произволен. Однако, работая с таблицей, мы должны действовать систематически. Мы могли бы взять три первых знака из каждой пятизначной последовательности, три средних знака, три последних знака или даже первый, второй и четвертый знаки. (Из первой пятизначной последовательности с помощью этих различных процедур получаются, соответственно, числа 100, 009, 097 и 109.) Мы могли бы применить эти процедуры в направлении справа налево, получив 790, 900, 001 и 791. Мы могли бы идти вдоль рядов, рассматривая поочередно каждую следующую цифру и игнорируя разбиение на пятерки (для первого ряда будут получены числа 100, 973, 253, 376 и 520). Мы могли бы иметь дело лишь с каждой третьей группой цифр (например, с 10097, 99019, 04805, 99970). Существует множество самых разнообразных возможностей, и каждая следующая ничуть не хуже предыдущей. Однако как только мы приняли решение о том или ином способе работы, мы должны систематически следовать ему, чтобы в максимальной степени соблюдать случайность элементов в таблице.
Таким образом, построение простой случайной выборки может оказаться совсем непростым делом. Кроме тех трудностей, которые мы еще будем обсуждать, данный метод требует большого объема технической работы, особенно когда речь идет о широкомасштабных исследованиях. По этой причине процедуры формирования случайной выборки часто видоизменяют, чтобы увеличить их возможности. Один из таких распространенных вариантов называется систематической случайной выборкой и используется тогда, когда мы хотим исследовать сравнительно большую совокупность, каждый член которой занесен в единый список, такой, как, например, телефонная книга, список студентов, список зарегистрированных избирателей, индекс или оглавление, повестка дня или [c.163] список членов какой-либо организации. Процедура выглядит следующим образом.
Подсчитайте (или оцените) количество объектов в совокупности и разделите его на желательное количество объектов в выборке (обсуждается ниже в данной главе). Если обозначить результат через k, то фактически можно сказать, что мы хотим выбрать один из каждых k объектов, или, говоря по-другому, каждый k-й объект. Это можно пояснить на конкретном примере.
Предположим, что из совокупности в 10 000 публичных заявлений, сделанных министерством обороны, мы хотим сформировать выборку размером в 500 документов; предположим также, что мы как свои пять пальцев знаем хронологический список, включающий все 10 000 документов. Чтобы отобрать систематическую случайную выборку:
1. Мы делим количество объектов в совокупности на желательный размер выборки, чтобы определить число k (в данном случае k= 10 000:500=20).
2. С помощью
таблицы случайных чисел мы выбираем номер объекта между 1 и k (в нашем примере между 1 и 20) для включения в нашу выборку.3. Мы движемся по списку документов, выбирая каждый k-й (двадцатый) объект.
Таким образом, если k равно 20 и мы пользуемся фрагментом таблицы случайных чисел, представленном на рис.5.2, начиная с верхнего левого угла таблицы, рассматривая двузначные числа (k в данном случае находится между 10 и 99) и используя только те элементы таблицы, которые соответствуют реальным номерам объектов (т.е. только те, которые находятся между 01 и 20), первым выбранным объектом будет 10. Мы, таким образом, включаем в нашу выборку объекты 10, 30 (10+k), 50 (10+2k), 70 (10+3k) и т.д., и так вплоть до объекта 9900 (10+499k). Эту верхнюю границу выборки можно задать в виде общей формулы j+(n–1)k, где j – первое случайное число, a n – желаемый объем выборки. Таким образом, можно воспользоваться
таблицей случайных чисел в сочетании с единым списком для формирования в целях осуществления анализа выборки объемом в 500 документов.Техника формирования систематической случайной выборки по сравнению с формированием простой случайной
[c.164] выборки имеет два важных преимущества: ее удобно применять по отношению к большим совокупностям, отвечающим условию наличия единого списка, и у нее много потенциальных возможностей использования. Тем не менее, применяя эту процедуру, мы должны иметь в виду одну очень важную ее особенность. Поскольку систематическая случайная выборка менее случайна, чем прямой выбор типа лотереи, в результате может быть получена менее репрезентативная подгруппа. Это можно проследить и на уровне определения, и на операциональном уровне.Прежде всего вспомним, что случайная выборка – это выборка, в которой каждый конкретный объект и каждое возможное сочетание из п объектов имеют равную вероятность быть выбранными. В систематической случайной выборке выполняется только одно из этих условий. Поскольку формирование такой выборки начинается с выбора по
таблице случайных чисел первого объекта, любой объект из совокупности в конечном счете имеет равные возможности войти в выборку (хотя и не обязательно при первой попытке, так как она осуществляется в пределах от 1 до k). Однако поскольку далее мы выбираем лишь объекты, отстоящие на k номеров один от другого, не всякое возможное сочетание оказывается допустимым. Так, в примере при k=20 в качестве первого можно выбрать любой объект от 1 до 20, но, как только выбран объект с номером 10, мы уже не можем включить объекты с номерами 9,14, 237 и 5 724 просто потому, что номера этих объектов не отличаются от 10 на целое число k. Следовательно, систематическая случайная выборка – это в лучшем случае лишь приближение к истинной случайной выборке.Данное наблюдение особенно важно, когда список, из которого производится выборка, характеризуется систематической направленностью. Для алфавитных и хронологических списков это обычно не существенно, однако для других типов списков может оказаться важным. Например, мы хотим измерить уровень умственных способностей в выборке, состоящей из учеников школы, в каждом классе которой 20 детей. В школе 100 классов, т.е. всего 2000 учеников. В ответ на нашу просьбу директор предоставляет список всех учеников школы, из которого мы собираемся извлечь выборку объемом в 100 человек. Однако перед нами не алфавитный
[c.165] список, а последовательность списков отдельных классов. Более того, список каждого класса дан не в алфавитном порядке, а соответствует положению, занимаемому учеником в классе: лучшие ученики идут вначале, и списки продолжаются в порядке убывания успехов. При таком положении дел, если выбирать каждого двадцатого (2000:100), начиная со случайным образом выбранного объекта под номером 1, мы получим выборку, состоящую из 100 лучших (и, возможно, самых умных) учеников школы. Если случайным образом будет выбран объект 10, в выборку попадут одни середняки. А если начать с объекта 20, то мы выберем лишь самых плохих учеников школы. Иными словами, внутренняя направленность, характеризующая список, на котором основана наша выборка, окажется причиной получения нерепрезентативной выборки. В конце концов все это приведет к тому, что мы либо не сможем обобщить наши результаты на генеральную совокупность, либо (если возникшая ситуация останется незамеченной) придем к потенциально неверным выводам. Хотя данный пример достаточно примитивен и приведен специально в целях иллюстрации, подобного рода списки, характеризующиеся определенной направленностью, действительно существуют, и исследователь, использующий процедуры, формирующие систематическую случайную выборку, должен быть подготовлен к таящейся здесь опасности.Таким образом, простая случайная выборка – это идеал, к которому мы стремимся, а систематическая случайная выборка – приближение к этому идеалу. Однако очень часто исследуемая ситуация такова, что не позволяет применить ни тот, ни другой метод. В особенности это касается случаев выборочного исследования. Ведь зачастую не бывает сведенных воедино списков совокупности, подлежащей изучению (так, например, не существует списка всех американских избирателей или всех жителей данного города), и даже количество (не говоря уже о конкретном составе) имеющихся объектов может быть заранее неизвестно. Таким образом, может оказаться невыполненным основное условие, необходимое для формирования простой или систематической случайной выборки, – наличие отдельных заранее идентифицируемых объектов. Более
[c.166] того, даже тогда, когда эта проблема может быть решена, технические трудности и ограниченные ресурсы могут привести к тому, что оба метода формирования выборки окажутся нереализуемыми. Это происходит потому, что случайный выбор конкретных объектов предполагает условие: в выборку должны быть включены определенные лица, – причем может оказаться, что они либо живут далеко друг от друга, либо с ними трудно поддерживать связь. Случайный в строгом смысле слова процесс не допускает никаких замен. Все эти факторы могут привести к таким огромным затратам времени и средств, при которых исследование вообще окажется невозможным.К счастью, существует другой метод, сохраняющий ценные для нас достоинства случайного выбора и лишенный большинства отмеченных недостатков. Этот метод (его называют либо методом
кластерной выборки, либо методом многоступенчатого случайного районирования) нашел широкое применение в выборочном исследовании. В основе многоступенчатой случайной районированной выборки лежит следующее соображение: вместо того чтобы считать в качестве членов выборки конкретных людей, будем рассматривать их как жителей того или иного пункта. Эта замена объясняется тем, что в отличие от людей, переезжающих с места на место, само по себе место жительства остается неизменным. Кроме того, расположение фактически любого места жительства в стране известно и нанесено на карту, каждое является частью различных географически определенных зон, таких, как кварталы, переписные участки, избирательные участки, законодательные округа, города, районы, округа, избирательные округа по выборам в конгресс и, наконец, штаты.Мы увидим, что некоторые из этих районов обладают свойствами, благоприятными для получения репрезентативной выборки. Пока же отметим, что, принимая во внимание жителя места, которое всегда остается постоянным, а не конкретного человека, который может быть более подвижным, мы оказываемся в состоянии стабилизировать и локализовать процедуру формирования выборки. Фактически мы просто даем другое определение нашему понятию совокупности. Вместо того чтобы говорить (если бы речь шла об исследовании
[c.167] в масштабах страны) обо всем населении, живущем в Соединенных Штатах, мы говорим об отдельных людях в местах их проживания. Поскольку с точки зрения любой практической цели между этими группами нет различий, мы можем сформировать выборку на основе второй группы и распространить полученные выводы на первую. Мы пользуемся гораздо более простыми и (по ряду причин, которые будут рассмотрены ниже) гораздо менее дорогостоящими методами выбора мест жительства, и тем не менее мы можем распространять наши выводы не на места жительства, а на населяющих их людей. В этом и состоит основная ценность многоступенчатой случайной районированной выборки.Сама эта процедура иллюстрируется на рис.5.3, где суммируется практика Центра выборочных исследований (ЦВИ) Мичиганского университета – основного национального центра по проведению выборочных исследований в политологии. Хотя в своих частностях процедура, используемая в ЦВИ, слегка отличается от той, которую будем описывать мы, обе они складываются из одних и тех же основных этапов. Итак, предположим, что мы собираемся проводить общенациональное выборочное исследование. Те процедуры, которые мы здесь рассматриваем, безусловно, могут быть применены в менее масштабных проектах.
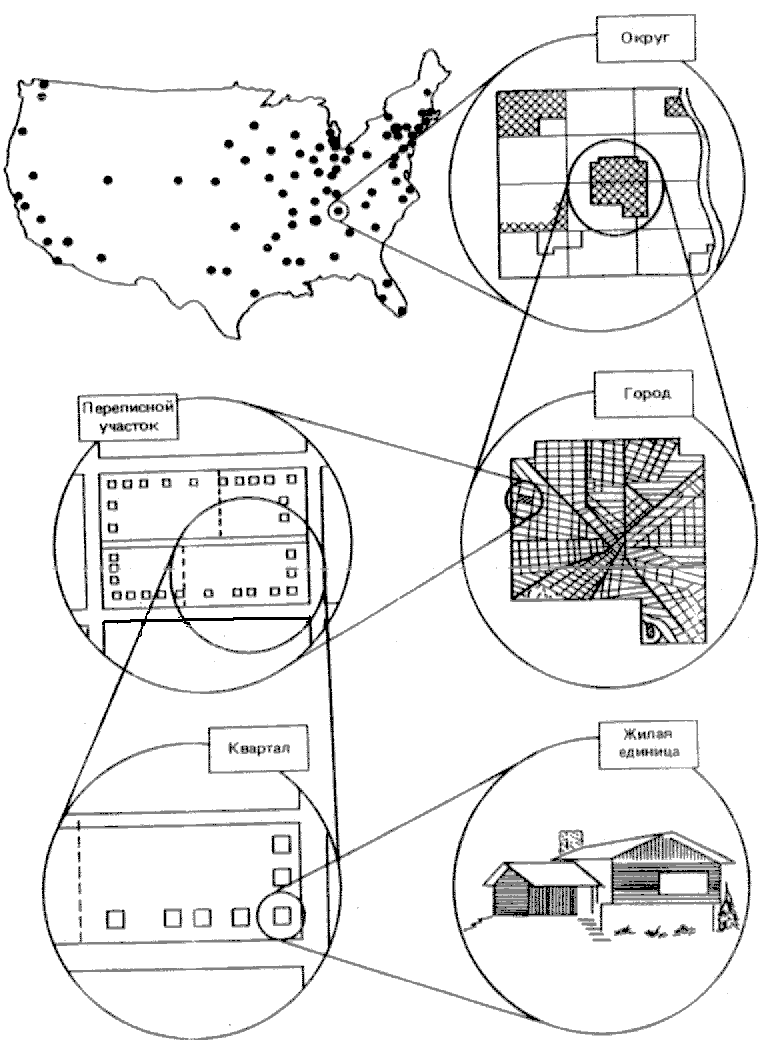
Рис. 5.3. Последовательность шагов в процессе многоступенчатой случайной районированной выборки (см.: Interviewer's Manual: Survey Research Center. –Ann Arbor: Institute for Social Research, University of Michigan, 1969. Р.8)
Начнем с того, что возьмем карту Соединенных Штатов и поделим ее на большое число районов с одинаковой численностью населения2. Это не так трудно, как кажется на первый взгляд, так как правительство уже осуществило такую (или по крайней мере близкую к нему) разбивку, образовав 435 избирательных округов по выборам в конгресс, население каждого из которых составляет немногим более полумиллиона человек. Мы приписываем каждому такому округу одно из чисел между 1 и 435 и, пользуясь
таблицей случайных чисел, отбираем для анализа несколько округов. Сколько именно округов будет выбрано, зависит как от предельного размера формируемой выборки, так и от имеющихся в нашем распоряжении ресурсов, но в целом, чем больше будет выбрано округов, тем лучше будет выборка. На этом этапе становится очевидной экономичность метода многоступенчатой случайной районированной выборки, поскольку, вместо того чтобы отыскивать [c.169] респондентов по всей стране, мы можем сконцентрировать наше внимание (и денежные средства) на сравнительно небольшом числе территорий, размеры которых в основном поддаются контролю. Таким образом, операции могут быть сосредоточены в нескольких местных отделах.Как только определены соответствующие округа, каждый из них далее подразделяется на еще меньшие по размеру, однако имеющие одинаковую численность населения территории. Зачастую они могут совпадать с существующими политическими образованиями, такими, как избирательные участки или избирательные округа. Затем эти избирательные участки подразделяются дальше – вначале на переписные участки, потом на кварталы и, наконец, на отдельные жилые единицы (дома и квартиры), – при этом на каждом этапе отбора используется процесс случайного выбора. В конце концов мы установим множество отдельных жилых единиц, количество которых приблизительно соответствует желательному объему нашей выборки. Их жители и будут объектами нашего исследования.
Существует тем не менее еще одна трудность: хотя обычно мы по ряду причин предпочитаем брать интервью лишь у одного лица по данному адресу, в каждом конкретном доме или квартире вполне может проживать несколько человек. У кого же брать интервью? Большинство исследователей, использующих такие процедуры формирования выборки, снабжают интервьюируемых рядом правил, регулирующих принятие решений на данном этапе, так чтобы в результате было получено множество квот на основе возраста, пола, и/или семейного положения респондента. В одном месте интервьюируемый может получить инструкцию выбрать самого младшего члена семьи мужского пола, в другом – самого старшего члена семьи женского пола и т.д. Во многих случаях искомый респондент определяется с помощью карт, подобных тем, что изображены на рис.5.4. Интервьюируемый получает несколько таких карт, в которых объект исследования устанавливается по-разному в зависимости от конкретного состава семьи; кроме того, он снабжается инструкцией последовательно использовать эти карты при переходе от одного интервью к другому.
[c.170]
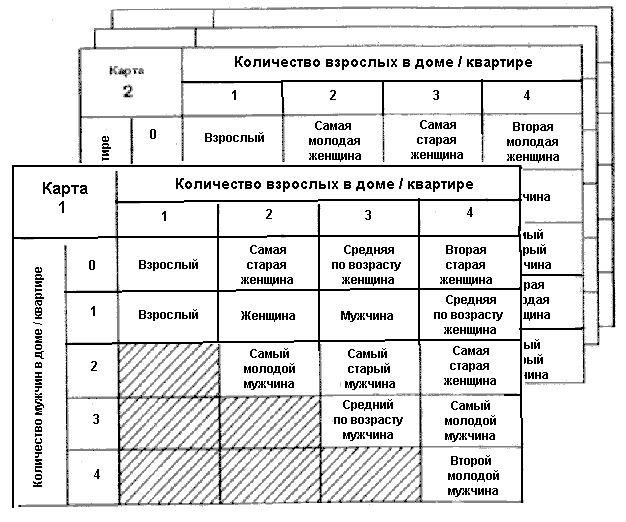
Рис. 5.4. Карты выбора респондентов
Таким образом, многоступенчатая случайная районированная выборка действительно наглядна. На каждом из этапов среди районов с одинаковым населением (либо среди районов, для которых вероятность быть выбранными устанавливается пропорционально их населению) осуществляется случайный выбор, пока наконец не устанавливаются отдельные жилые единицы. В каждом случае объектом процедуры выбора является географическая местность, и на каждом этапе определяется несколько групп местностей (отсюда и другой термин – кластерная выборка). Лишь на последнем этапе – этапе установления конкретных респондентов – процедура осуществляется с нарушением принципа случайности, однако на столь локальном уровне и с использованием столь аккуратно составленных квот, что воздействие на репрезентативность выборки, по всей вероятности, является при этом минимальным. Во многих случаях многоступенчатая случайная районированная выборка (так же как аналогичные
[c.171] процедуры выбора, используемые при выборочном обследовании) дает приемлемое приближение к действительно случайной выборке при небольших затратах времени и средств.Необходимо упомянуть еще один метод, хотя это скорее не процедура выбора, а всего лишь стратегия. Этот метод известен под названием
стратифицированного формирования выборки и используется в первую очередь тогда, когда мы хотим детально исследовать некоторую подгруппу совокупности, которая так мала, что случайная выборка будет содержать слишком небольшое для такого анализа количество членов этой подгруппы.Предположим, к примеру, что мы хотим проверить гипотезу, согласно которой, в течение первых двух месяцев своего правления (периода, часто называемого “медовым месяцем”) президенты более откровенны со средствами массовой информации, чем когда бы то ни было в дальнейшем, и что для проверки этой гипотезы мы собираемся анализировать содержание стенограмм пресс-конференций президентов. Предположим далее, что за некоторый период времени в нашем распоряжении имеется 500 таких стенограмм и лишь 25 из них представляют пресс-конференции периода “медового месяца” и что мы хотим включить в выборку всего 100 пресс-конференций. Если использовать в этом случае простой или систематический случайный выбор, можно ожидать, что в выборку будет входить приблизительно 5 стенограмм периода “медового месяца” и приблизительно 95 стенограмм последующего периода. Столь небольшое число стенограмм первого типа очень затрудняет осмысленное сравнение, поскольку при этом может оказаться слишком мало примеров, которые бы давали точную картину ответов президента на вопросы журналистов.
В таких условиях, когда мы хотим повысить значимость (придать больший вес) определенной подгруппы, мы применяем метод стратификации. Поступая таким образом, мыв действительности формируем не одну, а две отдельные выборки. Первая – это простая или систематическая случайная выборка для меньшей подгруппы (стенограммы периода “медового месяца”), и по объему она будет больше, чем ожидалось, в соответствии с частотой появления этой подгруппы в исходной выборке (в нашем
[c.172] примере это будет не 5, а, скажем, 15 объектов). Вторая – это простая или систематическая случайная выборка для большей подгруппы (стенограммы всех периодов, следующих после “медового месяца”), и по объему она будет меньше, чем ожидалось, в соответствии с частотой появления в исходной выборке (в нашем примере – 85, а не 95 объектов). В данном случае выборку можно назвать стратифицированной относительно времени проведения пресс-конференции. В результате мы получим относительно больше объектов из числа стенограмм периода “медового месяца” для анализа и сопоставления со стенограммами более поздних периодов, чем могли бы отобрать, используя другие методы.Здесь следует сделать три замечания. Во-первых, стратификация не заменяет простой случайный выбор или какой-либо иной вид выбора, а представляет собой дополнительную возможность, используемую в определенных обстоятельствах. Фактически это процедура формирования выборки второго порядка. При этих условиях стратификация используется достаточно часто, в особенности при опросе общественного мнения, на последних этапах формирования выборки, чтобы обеспечить, к примеру, необходимое равновесие между количеством мужчин и количеством женщин. Таким образом, по своему назначению стратификация очень напоминает квоты, которые используются на последнем этапе многоступенчатой районированной выборки.
Во-вторых, поскольку стратификация требует формирования отдельных выборок, она может использоваться лишь там, где мы в состоянии заранее установить релевантные субсовокупности. В нашем примере это не составляет труда, поскольку до начала формирования выборки мы легко можем отличить стенограммы периода “медового месяца” от стенограмм более поздних периодов. Однако во многих выборочных обследованиях, там, где мы, быть может, захотели бы провести стратификацию, опираясь на менее очевидные переменные, нас могут ожидать большие трудности.
В-третьих, поскольку при стратифицированном формировании выборки используются отдельные выборки и поскольку единственное, что мы в состоянии сделать, – это распространить результаты, полученные на данной
[c.173] выборке, на ту самую совокупность (или субсовокупность), из которой она извлечена, мы должны с очень большой осторожностью делать выводы на основании исследования, базирующегося на такой выборке. Причина этого вполне ясна: проводя стратификацию с целью повышения в нашем исследовании количества объектов определенного типа, мы фактически смещаем всю выборку в сторону этих объектов.Чтобы преодолеть это смещение, следует формулировать наши выводы одним из двух единственно возможных способов. Во-первых, мы можем сопоставить друг с другом результаты, полученные для групп, по которым проведена стратификация (например, можем сопоставить результаты для пресс-конференций периода “медового месяца” с результатами для пресс-конференций более поздних периодов). В этом случае мы просто сравниваем результаты для отдельных выборок, не делая никаких выводов о пресс-конференциях в целом. Во-вторых, мы можем приписать разный вес группам, по которым проведена стратификация, пропорционально их доле в совокупности и затем сделать выводы относительно всей совокупности. В этом случае мы в полной мере используем имеющиеся в нашем распоряжении подробные сведения о меньшей подгруппе (пресс-конференциях периода “медового месяца”), но уменьшаем их роль в совокупности всех пресс-конференций (точнее, восстанавливаем правильное соотношение). При использовании данной процедуры стратифицированная выборка может служить в качестве приближения к простой случайной выборке, давая при этом более полную информацию.
Иногда более полезными могут оказаться другие виды выборок. Одна из них – это
квотная выборка, когда члены совокупности классифицируются в соответствии с несколькими релевантными характеристиками (такими, как пол, возраст или идентификация партийной принадлежности) и лица, обладающие такими свойствами, отбираются в количестве, пропорциональном их доле в совокупности. Еще один тип – это экспертная выборка, когда наблюдатель просто выбирает те объекты, которые он по какой-то причине считает типичными или репрезентативными для той совокупности, из которой они извлечены. Такая выборка чаще всего используется при исследовании [c.174] небольших совокупностей и элитарных или специализированных групп. Необходимо, однако, помнить, что такого рода выборки не являются действительно репрезентативными для соответствующих совокупностей (в самом деле, в противоположность случайным выборкам вероятность и степень репрезентативности этих выборок неопределенны) и поэтому они менее предпочтительны. [c.175]УСТАНОВЛЕНИЕ НЕОБХОДИМОГО ОБЪЕМА ВЫБОРКИ
После того как определены термины и рассмотрены процедуры выбора, остается обсудить последний вопрос: каким образом следует решать, сколько выбрать объектов. Ответ на этот вопрос в значительной степени требует привлечения сложных статистических понятий, которые мы не в состоянии обсуждать в рамках настоящей книги. По этой причине часть из того, о чем говорится в данном разделе, должна быть принята на веру, хотя в конце главы мы все-таки указываем некоторые книги, в которых эти проблемы обсуждаются. Спешим, однако, подчеркнуть, что большинство соображений, лежащих в основе определения необходимого объема выборки, понять достаточно просто и, прежде чем двигаться дальше, стоит уделить им немного внимания.
Чтобы установить необходимый объем выборки следует учесть несколько факторов. Один из наиболее важных –
гомогенность – степень близости друг к другу членов данной совокупности с точки зрения изучаемых нами характеристик. Если каждый индивидуум в совокупности в точности такой же, как все остальные, то, выбрав всего лишь одного из них, мы получим действительно репрезентативную выборку. Напротив, если каждый индивидуум в совокупности абсолютно не похож ни на какой другой, то, прежде чем мы сможем утверждать, что у нас имеется репрезентативная выборка, нам потребуется провести перепись всей совокупности. В первом случае совокупность называют полностью гомогенной, во втором–полностью гетерогенной. Разумеется, в действительности большинство совокупностей располагается между этими двумя полюсами.Чем гомогенное данная совокупность, т.е. чем меньше различий между ее членами, тем меньшая по объему выборка необходима для ее представления. Напротив, чем гетерогеннее совокупность, т.е. чем больше различий
[c.175] между ее членами, тем большая выборка необходима для ее представления. Это особенно важно учитывать при стратифицированном формировании выборки, поскольку самим актом стратификации мы создаем подгруппы, более гомогенные, чем совокупность в целом. Таким образом, внутри уровней можно использовать, не теряя при этом репрезентативности, выборки меньшего объема, чем следовало бы для всей совокупности.Сходным образом, чем больше категорий мы хотим исследовать, тем больше должна быть выборка. Это вполне естественно, поскольку, увеличивая разнообразие и тонкость наших измерений, мы подчеркиваем гетерогенность исследуемой совокупности. Иными словами, чем больше вопросов мы задаем и чем больше типов ответов допускаем, тем больше вероятность того, что мы обнаружим различия между исследуемыми объектами. Чем больше различий между объектами мы принимаем во внимание, тем больше объектов мы должны изучить, чтобы выборка получилась репрезентативной.
Еще одно важное соображение касается степени точности, которая нам требуется. Мы используем выборку для оценки характеристик больших совокупностей, однако любая оценка может содержать ошибку. Какую ошибку выборки мы готовы допустить? Ответ часто зависит от предполагаемого использования результатов. Если мы получаем деньги за то, что проводим опрос общественного мнения для предсказания результатов выборов, в которых участвуют кандидаты с близкими шансами, мы, скорее всего, захотим иметь минимальную величину ошибки. Если же мы политологи и пытаемся раскрыть основные тенденции в области отношений и поступков людей, мы, видимо, согласимся допустить существенно большую величину ошибки. Вообще, чем большая точность нам требуется, тем больше должна быть наша выборка.
С этой же проблемой связан и второй вопрос: насколько мы можем быть уверены в правильности нашей оценки величины ошибки выборки? Читателю, недостаточно искушенному в статистике, возможно, непросто понять приводимые в этом случае доводы, однако предлагаемый ниже пример может кое-что прояснить. Здесь существенны следующие моменты. Каждая выборка дает нам некоторую оценку характеристик совокупности, однако вследствие
[c.176] того, что никакие две выборки не будут в точности одинаковы, эти оценки будут несколько отличаться одна от другой и от оценки совокупности в целом. Это последнее отличие и есть ошибка выборки. Большинство выборок данного объема, взятых из одних и тех же совокупностей, будут очень похожи друг на друга и на саму совокупность, однако может случиться и так, что сформированная выборка будет отличаться от прочих. Может оказаться, что входящие в ее состав женщины, пожилые люди, республиканцы, выпускники колледжей и т.п. включены в таком количестве, которое не отражает реальной доли этих групп в соответствующих совокупностях. Такая выборка, естественно, не будет репрезентативной: она выйдет за рамки допустимой величины ошибки.Проблема заключается в том, что в реальной действительности мы не всегда знаем внутренние параметры совокупности, для оценки которых предназначена наша выборка (зачастую установление таких параметров и является целью исследования); кроме того, мы формируем не множество выборок, а всего лишь одну. И хотя мы сумеем проконтролировать очевидную валидность нашей выборки, проведя сравнение с другими исследованиями той же самой совокупности или совокупности, похожей на данную, мы
не можем быть уверены, что наша выборка не случайное исключение, что она нерепрезентативна (это мало вероятно, но возможно). Однако из занятий статистикой нам известно, что вероятность вытащить из горы яблок гнилое, можно снизить, если увеличить объем выборки. Чем больше объектов мы включим, тем выше вероятность того, что будет получена истинно репрезентативная выборка, которая действительно не выйдет за рамки заданной нами величины ошибки.Наши рассуждения можно сделать менее абстрактными, если рассмотреть краткие характеристики выборок разного объема, представленные в табл.5.1. Эти характеристики получены на основе более обширных сведений, содержащихся в табл.
А.2 и А.3 приложения А. В табл.5.1 перечислены минимальные объемы выборок, соответствующие нескольким уровням ошибки выборки, и степени уверенности для случая простой случайной выборки при относительно гетерогенной совокупности объемом более 100 000 объектов. (Изучение таблиц приложения А, [c.177] послуживших источником для данной таблицы, показывает, что при формировании выборок для меньших совокупностей приводимые цифры могут быть несколько уменьшены, однако при возрастании объема совокупности приводимые значения задают предельный объем выборки.)Таблица 5.1
Краткие характеристики выборок разного объема
|
Допустимый процент ошибки выборки |
Степень уверенности |
+ |
|
0,95 |
0,99* |
|
|
± 1 |
10 000 |
22 500 |
|
± 2 |
2 500 |
5 625 |
|
± 3 |
1 111 |
2 500 |
|
± 4 |
625 |
1 406 |
|
± 5 |
400 |
900 |
|
± 10 |
100 |
– |
*
Для большей наглядности имеющееся в исходной таблице значение 0,997 округлено до 0,99.
Возможно использовать эти три таблицы каждым из двух методов.
Мы, возможно, захотим задать определенный уровень ошибки выборки, который мы согласны допустить, и степень уверенности, с которой будем действовать. Предположим, что взяты, соответственно, числа ±4% и 0,99. Первое число означает, что любое измерение, которое мы могли бы произвести в нашей выборке, отклоняется не более чем на четыре процента вверх или вниз от истинного значения того же признака в более обширной совокупности. Если, например, мы устанавливаем, что в проводимом исследовании 43% респондентов сообщают о своей солидарности с демократической партией, мы будем считать, что в случае полной переписи населения реальное количество приверженцев демократической партии будет составлять 43% ± 4% или находиться в пределах приблизительно от 39 до 47%. В соответствии с таблицей (если посмотреть на пересечение строки ± 4% и столбца 0,99) для достижения данной степени точности с уверенностью 99% мы должны иметь выборку, состоящую по крайней мере из 1406 объектов. Если мы хотим уменьшить величину ошибки (повысить точность) до, скажем, ± 2%
[c.178] (т.е. оценить количество демократов более точно, в пределах от 41 до 45%), мы должны увеличить объем выборки по крайней мере до 5625 объектов. Из таблицы отчетливо видно, что при любой степени уверенности повышение точности требует увеличения выборки.Второе число, о котом мы говорили, обозначает вероятность того, что наша выборка действительно репрезентативна для более обширной совокупности в рамках заданной степени точности. В данном контексте 0,95 (95% уверенности) означает, что из 100 выборок данного объема, полученных из одной и той же совокупности, 95 выдержат тест на точность, а 0,99 (99% уверенности) означает, что 99 из 100 выборок данного объема, полученных из одной и той же совокупности, будут точны настолько, насколько это было предсказано. Таким образом, вероятность того, что любая конкретная выборка будет давать желаемую точность, равна, соответственно, 95:5 (т.е. 19:1) и 99:1.
Как и следовало ожидать, для каждого уровня ошибки выборки необходимый объем выборки значительно больше в том случае, когда мы хотим достичь 99, а не 95% уверенности. Так, в нашем примере с демократами видно, что при величине ошибки 4% выборка объемом 625 объектов позволяет с 95%-ной уверенностью утверждать, что доля демократов среди населения находится где-то между 39 и 47%, тогда как то же самое утверждение с 99%-ной уверенностью требует выборки объемом по меньшей мере 1406 объектов. Вообще говоря, чем ниже ошибка выборки и чем выше степень уверенности, тем лучше будет то исследование, которое мы проводим. Для политологического исследования степень уверенности 0,95 или 0,99 принято считать вполне приемлемой.
Таблицу такого вида можно использовать иначе. Если, к примеру, мы анализируем исследование, в котором используется выборка, состоящая из 2500 объектов, то тогда можно обратиться к таблице и установить ошибку выборки и степень уверенности. Посмотрев в табл.5.1, видим, что интерпретация может быть неоднозначной. Мы можем считать, что 2500 объектов дают ошибку выборки ± 3% с уверенностью 0,99 или ошибка выборки ±2% с уверенностью 0,95. Каждая из этих интерпретаций в равной степени приемлема, а вместе они помогают прояснить взаимоотношения между точностью и
[c.179] уверенностью. При одном и том же количестве объектов мы будем в состоянии располагать высокой степенью уверенности относительно менее точного результата или несколько меньшей степенью уверенности относительно более высокой точности. Однако нельзя одновременно и вкушать от пирога исследования, и оставлять его нетронутым.Конечно, в идеале мы всегда предпочитаем действовать с минимальными ошибками и с максимальной уверенностью. К сожалению, в дело часто вмешиваются практические соображения. Например, стоимость одного личного интервью в исследовательском проекте может равняться 50 долларам, включая собственно расходы на интервью, расходы на транспорт и пр. Это означает, что при 99%-ной уверенности стоимость снижения величины ошибки с ±3 до ±2% может составлять 130 000 долларов. Во многих случаях различие в качестве результатов не стоит производимых дополнительных затрат, а в гораздо большем числе случаев средств просто нет. Таким образом, важную роль в ограничении объема выборки играют ограничения на ресурсы. В большинстве наиболее значительных опросов общественного мнения, а также в большинстве наиболее значительных исследовательских проектов в области политологам используются выборки объемом приблизительно 1400–1600 респондентов. Такие исследования дают результаты с точностью 3–4% и со степенью уверенности 0,99 и считаются одновременно и возможными, и достаточно точными. Проекты, использующие контент-анализ или другие относительно менее дорогостоящие методы сбора данных, часто тяготеют к верхнему правому углу таблицы.
Прежде чем мы завершим обсуждение проблемы объема выборки, следует затронуть еще один вопрос, хотя он, несомненно, менее очевиден и интуитивно менее привлекателен, чем все то, о чем мы говорили ранее. Внимательное изучение табл.
А.2 и A.3 приложения А показывает, что, достигнув определенного предела, размер совокупности не влияет на объем выборки, которая должна ее представлять. В то время как доказательство этого утверждения выходит за рамки настоящей книги, вытекающие из него следствия касаются нас вплотную. Ведь, в сущности, наличие такого верхнего предела означает, что практически одна и та же выборка, если она должным образом [c.180] сформирована, может быть в равной степени репрезентативна для населения г.Роанока (штат Виргиния), г. Нью-Йорка, Соединенных Штатов и всего Западного полушария. Размер совокупности является важным фактором при определении объема выборки лишь в случае относительно небольших совокупностей.Итак, подводя итоги, следует подчеркнуть, что, формируя выборку, необходимо очень внимательно следить за тем, чтобы не только отобрать из данной совокупности достаточное количество объектов, но и взять такую группу, которая, как представляется, будет действительно репрезентативной с точки зрения распределения характеристик внутри данной совокупности. Должное внимание на этом этапе процесса исследования в дальнейшем окупится сторицей. Наоборот, небрежность при формировании выборки может нанести непоправимый вред любому исследованию.
[c.181]Начинающий политолог часто упускает из виду один важный момент: каждый раз, когда осуществляется сбор данных любым методом и из любого источника, у исследователя появляется соблазн распространить свои выводы на все остальные объекты. Именно для того, чтобы подчеркнуть этот факт, мы предпочли обсудить проблему формирования выборки здесь, а не в разделе, посвященном выборочному обследованию. Что бы ни было объектом исследования: события, политические заявления, подборки новостей, политические юрисдикции, организации, общественное мнение или любые другие интересующие вас вопросы, – важно понимать определяющую роль процесса отбора и его влияние на значимость и полезность исследования.
[c.181]
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА К ГЛАВЕ 5
Статистические процедуры, лежащие в основе определения нужного объема выборки, рассматриваются в ряде изданий, к числу которых относятся:
Вlаlосk H.M., Jr. Social Statistics. – N.Y.: McGraw-Hill, 1979, 2nd ed., chap. 9; Palumbо D.J. Statistics in Political and Behavioral Science. –N. Y.: Columbia University Press, 1977; 2nd ed.; Yamane T. Elementary Sampling Theory. – Englewood Cliffs (NJ.): Prentice-Hall, 1967.О практическом применении многоступенчатой случайной районированной выборки можно прочесть в: Веrelsоn В.R. et al. Voting: A Study of Opinion Formation in a Presidental Campaign. – Chicago: University of Chicago Press, 1954, app. C, – а более детальное описание того же применения данной процедуры имеется в: Interviewer's Manual: Survey Research Center. – Ann Arbor Institute for Social Research, University of Michigan, 1976, sec. С; в кн.: Jacob C.H. Debtors in Court: The Consumption of Government
Services. – Chicago: Rand McNally, 1969, app. В, – предлагаются примеры формирования случайной выборки, а в кн.: Patterson Th.E., McClure R.D. The Unseeing Eye: The Myth of Television Power in National Elections. – N.Y.: Putnam, 1976, app. В., – рассматривается использование многоступенчатой случайной районированной выборки в городе, определенном экспертным путем. Проблема формирования децентрализованной совокупности затрагивается в: Johnstone J.W.С. et al. The News People: A Sociological Portrait of American Journalists and Their Work. – Urbana: University of Illinois Press, 1976, ch. 1. Другие примеры процедур выборки регулярно публикуются на страницах журнала “Public Opinion Quarterly”.Несколько вариантов каждого из этих методов выборки описывается в: Miller D.C. Handbook of Research Design and Social Measurement. – NewburyPark, Calif.: Sage, 1991; 5th ed. [c.182]