Наблюдая проявления признаков (Х_i) в выборочной совокупности, состоящей из n носителей (конкретных людей: жителей города, села, профессионально-занятых в какой-либо сфере, обучающихся и т.п.), говоря языком теории вероятностей, мы проводим n независимых испытаний, (опытов) в которых конкретное проявление признака (X_i)  есть или нет в каждом из опытов. То есть в основу исследования ложится испытание Бернулли - независимые испытания с двумя случайными исходами: “удачей” и “неудачей”. Их вероятности изменяются от испытания к испытанию. Вероятность “успеха” - p, а вероятность “неуспеха”-  q = 1 - p. Для дискретной случайной величины вероятность проявления признака X_i точно m раз в n  независимых опытах равна:

                                                                                                        

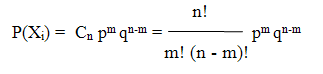
Эта формула называется биноминальным законом распределения Бернулли.[1] Биноминальное распределение при соответствующих условиях и достаточно больших значениях n можно заменить подходящим нормальным распределением.[2]

Под вероятностью события в статистическом смысле понимается почти достоверный предел его относительной частоты (частости) при неограниченно растущем числе испытаний:[3]

                                                                                            

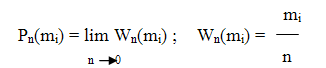
 В реальности наблюдать у всей генеральной совокупности (N) проявление признака (X_i) практически бывает невозможным да и не нужным. То есть необходимо ограничиваться каким-то разумным числом n<N, чтобы с определенной степени достоверности говорить о свойствах генеральной совокупности (N) на основе описания свойств выборочной (n). Говоря языком математики, чтобы уверенно применить эмпирическую функцию распределения (W_n), необходимо иметь оценку разности между точным и приближенным выражением функции.[4] Модуль разности между P_n и W_n называется абсолютной погрешностью выборки:[5]

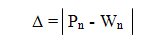
Абсолютная погрешность не характеризует точности измерения. Например, при измерении длины стола в 2 м и длины дороги в 200 км допущена абсолютная погрешность D₁= D₂=0.1 м.[6] Для оценки точности измерения используется относительная погрешность (d) применяемого значения W_n, равная отношению абсолютного значения погрешности этого числа к абсолютной величине соответствующего точного числа:[7]

                                     

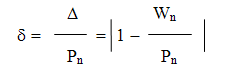
  Следовательно, чтобы определить объем выборочной совокупности необходимо провести оценивание возможного эмпирического распределения, то есть извлечь из данных наилучшее статистическое приближение для неизвестных значений параметров, отвечающих наблюдениям, а также объективную меру этого распределения.[8]

Для этого необходимо уточнить методы описания выборок, которые аналогичны основным методам статистического описания совокупности. Основными из них являются:

прямое или косвенное описание полного распределения: прямое - в терминах одной из стандартных производящих функций;

описание отдельных свойств полного распределения, таких как  моменты (дисперсия, вариация, ковариация), избранные процентные точки.[9]

Например, используя второй метод описания первых моментов и избранных процентных точек и определив достаточным интервал доверия с коэффициентом равным 0.9, можно вычислить объем выборки. При этом, во-первых, определив по таблице критическую точку 100%  распределения при обозначенном коэффициенте доверия (t=1.65)[10]; во-вторых, определив как возможно максимальную дисперсию качественного дихотомического вопроса (да или нет) d²_max= p q = 0.25; в-третьих, определив абсолютную ошибку (погрешность) выборки D = 1 - 0.9 = 0.1.

Для определения объема выборки используем формулу для случайного повторного отбора, когда объем генеральной совокупности неизвестен:[11]

                                                       

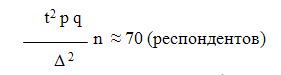
        Для обработки эмпирических данных необходимо определить, доверительный интервал для математического ожидания эмпирической функции распределения, используя при этом второй метод оценивания,[12] предварительно вычислив предельную ошибку выборочной средней для максимально возможной дисперсии D(X_i) = d²= 0.25:[13]

                                                        

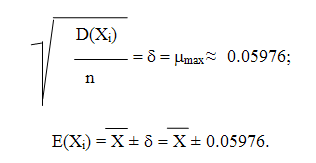
        Таким образом, что бы выводы исследования можно было распространить на исследуемую совокупность, ее объем должен быть в соответствии закону больших чисел не менее 70 обследуемых для коэффициента доверия, равного 0.9. Обосновав логико-математически требуемое количество респондентов в выборочной совокупности, необходимо определить логико-структурный состав выборки, то есть определить в ней представительство конкретных людей количественно и качественно.

Выборка это процесс формирования выборочной совокупности путем отбора единиц наблюдения.

Единицы наблюдения включают в себя:

Элементы выборочной совокупности (например, респонденты), подлежащие изучению, это  единицы анализа;

Элементы (поселения, предприятия, группы респондентов), отбираемые на каждом этапе выборки по особому плану, это единицы отбора.

        Выборочная совокупность это часть генеральной совокупности, отражающая основные с точки зрения целей исследования свойства, признаки генеральной совокупности.

Свойство выборочной совокупности воспроизводства характеристик генеральной совокупности называется репрезентативностью. Ее критерии: статистический - отражение при расчете объема выборки в выборочной совокупности параметров генеральной с заданной погрешностью; ресурсно-экономический - экономичность исследования (оценка кадрового обеспечения, стоимости, временных затрат и т.д.); аналитический - ограничения на объем выборки, накладываемые задачами последующего анализа.

Генеральная совокупность это общность людей или социальный объект, на который распространяются выводы исследования.

Выборка бывает одноступенчатая (на первой ступени объекты репрезентации совпадают с единицами наблюдения) и многоступенчатая (отбор на первой ступени объектов репрезентации, на последующих единиц наблюдения).

Случайным называется отбор, при котором  каждая единица генеральной совокупности имеет равную или почти равную вероятность попадания в выборочную совокупность. Случайные отборы бывают:

Вероятностный отбор - при котором каждая единица генеральной совокупности сохраняет равную возможность на протяжении всего процесса отбора  быть отобранной в выборочную совокупность (повторный отбор) или вероятность попадания возрастает, так как отобранная единица не участвует в отборе далее (бесповторный отбор). Основное требование - достаточно большой объем выборочной совокупности;

Систематический отбор это случайный отбор, при котором первая единица наблюдения отбирается случайно, а остальные через один и тот же интервал (шаг), например из списка. Это псевдослучайный отбор.

Направленным называется неслучайный отбор, при котором единицы наблюдения отбираются в выборочную совокупность в соответствии с критериями, заданными исследователем. Направленные отборы бывают:

Гнездовой отбор это направленный многоступенчатый отбор, при котором на каждой ступени выделяется промежуточный объект репрезентации (“гнездо”), служащий исходной совокупностью для следующей ступени. При его осуществлении, как правило, в качестве единиц отбора выступают не отдельные респонденты, а группы с последующим сплошным отбором их. Особенностью является то, что “гнезда” на каждой ступени неоднородны по внутренней структуре подобно генеральной совокупности. Респондентом называется лицо (личность, человек), которое является источником первичной социологической информации, представляющей собой результат измерения;

Квотный отбор это направленный многоступенчатый отбор, при котором единицы наблюдения включаются в выборочную совокупность пропорционально их долям (“квотам”) в генеральной совокупности. Ему предшествует построение генеральной совокупности, воспроизводящей ее структуру в виде пропорций (квот) изучаемый признаков, например, если в коллективе количество мужчин и женщин соотносится как 1:2, то в выборочной совокупности должны быть представлены респонденты по этому признаку в таком же соотношении. Это наиболее сложный метод, применяемый при большой генеральной совокупности и требующий для отбора респондентов использования не менее четырех признаков;

Районированный отбор это направленный многоступенчатый отбор, которому предшествует процедура деления совокупности на “районы”, которые внутри себя относительно однородны, но различаются между собой. Основные особенности - деление производится на основе признака, коррелирующего с исследуемыми характеристиками; ошибка выборки обуславливается только вариацией внутри выделенных типичный групп (районов). Данный отбор требует информации о генеральной совокупности для определения %-ного  представительства признаков деления в выборочной совокупности, предварительного анализа объекта исследования;

Метод основного массива это направленный отбор, при котором наблюдению подвергается группа единиц генеральной совокупности, удельный вес которых вполне достаточен (достаточно велик) по мнению исследователя. Основным условием применения выступает доказательность того, что оставшаяся, не подвергшаяся исследованию часть генеральной совокупности не окажет существенного влияния на конечные выводы, это, как правило, 70%  объема генеральной совокупности;

Стихийный отбор это направленный отбор, при котором нельзя обеспечить соответствие выборочной совокупности генеральной по всем изучаемым признакам или нельзя уточнить выборочную совокупность: отбор “первого встречного” - направленный по месту и времени единиц наблюдения в многолюдных местах;  отбор “себе подобных” - отбор из своего ближайшего наблюдения; прессовый отбор - респонденты сами “включаются“ в выборочную совокупность на основе теле опросов, радио опросов, анкет, публикуемых в печати и т.д.

Основными ошибками социологического исследования являются: теоретические (связанные с выбранной теорией), статистические (как правило, это заданная погрешность), наблюдения (полученные при сборе и первичной обработке информации). Ошибки наблюдения бывают: ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают в результате неправильного установления фактов в процессе наблюдения или не точной их записи: случайные  - при заполнении документов, при измерении показателей, при подсчете и т.п.; систематические - из-за неправильного выбора метода сбора или обработки первичных данных, неточностью в “инструменте” (анкете, бланке наблюдения и т.д.), из-за не учета постоянного влияния внешних факторов и т.п. Ошибки репрезентативности возникают из-за отклонения значений показателей по выборочной совокупности от их значений по генеральной: случайные - при отборе единиц наблюдения (как правило, задаются при определении объема выборки); систематические - из-за неточности соблюдения процедуры выборки, отказа респондентов, нарушений процедуры обработки.

Таким образом, эмпирическое исследование открывает новые факты и ставит новые задачи перед теорией. Теоретическое исследование получает новые возможности объяснения фактов и методологически ориентирует эмпирическое. В сущности, это два уровня глубины научного исследования социальных процессов и явлений. Единство и взаимообусловленность эмпирического и теоретического уровней  являются основной теоретико-методологической предпосылкой и условием достоверности получаемого социологического знания. Социологическое исследование это система логически последовательных методологических и организационно-технических процедур, связанных между собой единой целью - получить объективно-достоверные сведения об изучаемом социальном явлении или процессе для их последующего использования на практике.